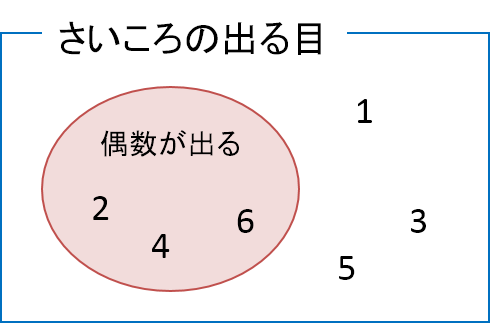
集合を視覚的に表す場合、「ベン図」が用いられることがあります。例えば、さいころを投げた場合に偶数の目が出る事象Aをベン図で表すと次のようになります。

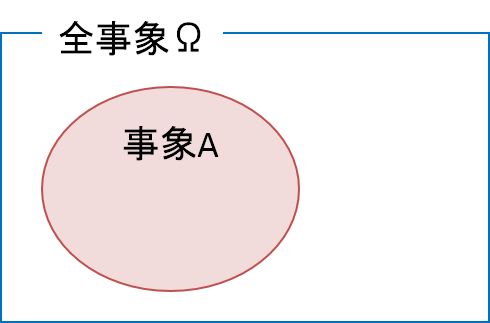
で囲まれた四角が全事象を表します。つまり、この四角の中にサイコロの6つの目である「1, 2, 3, 4, 5, 6」が含まれます。このうち、事象Aに含まれるものは、偶数の目である「2, 4, 6」です。したがって、これらは事象Aの円の中に含まれます。

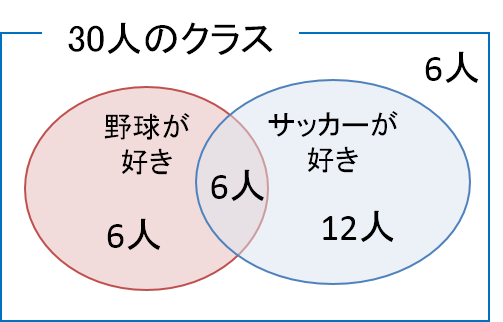
別の例を見てみます。30人のクラスで好きなスポーツを集計したところ、次のようになりました。この結果をベン図で表してみます。

• 野球が好き：12人
• サッカーが好き：18人
• 野球もサッカーも好き：6人

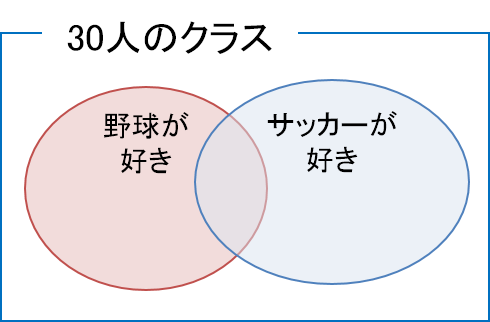
この結果には2つの事象が含まれます。「野球が好き」が1つ目の事象、「サッカーが好き」が2つ目の事象です。これら2つの事象を同時に満たす事象（野球もサッカーも好き）があることから、2つの円は次の図に示すように重なります。

この2つの円が重なった部分の事象にあてはまる人数は6人です。したがって、野球だけが好きな人は12－6=6人、サッカーだけ好きな人は18－6＝12人となります。これらの値をベン図に書き入れると次のようになります。

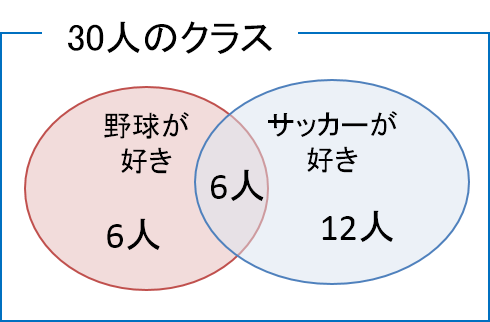
また、これらの2つの円の外に属する人は、野球もサッカーも好きではない人の集合になります。この人数はベン図より、30－6－6－12=6人となります。このベン図に示されている全ての人数を足し合わせると全集合である30人になります。