- Step2. 中級編
- 1. 2×2のクロス集計表と様々な比率
1-3. オッズ比1
2つの異なる群においてある事象が起こる確率をそれぞれ、![]() 、
、![]() としたとき、2つの群のオッズ
としたとき、2つの群のオッズ ![]() 、
、![]() の比をオッズ比といいます。オッズ比は次の式から計算することができます。
の比をオッズ比といいます。オッズ比は次の式から計算することができます。
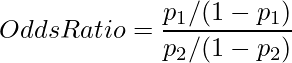
オッズは、ある事象が起こらない確率に対するその事象が起こる確率の比であり、「ある事象の起こりやすさ」を表します。ある事象が起こらない確率と起こる確率が等しい場合には、オッズは1になります。
オッズ比は、2つの群におけるオッズを比較したものであり、「ある群における事象の起こりやすさに対する別の群における事象の起こりやすさ」を表します。2つの群で事象の起こりやすさが等しい場合には、オッズ比は1になります。ある群(分子の群)における事象の起こりやすさが別の群(分母の群)よりも大きい場合には、オッズ比は1より大きくなります。
この式から分かるように、オッズ、オッズ比ともに常に正の値を取ります。
■オッズ比の使い方
オッズ比は医学や薬学の分野で、2変数間のリスクを比べるときによく用いられます。臨床試験やコホート研究など前向き研究のときはリスク比が使われますが、ケースコントロール研究など後ろ向き研究のときにはオッズ比が使われます(研究デザインの詳細については16-4章を参照)。
まず、前向き研究の例を考えてみます。
| がんの罹患あり | がんの罹患なし | 合計 | |
|---|---|---|---|
| 飲酒あり | 20 | 80 | 100 |
| 飲酒なし | 10 | 190 | 200 |
| 合計 | 30 | 270 | 300 |
この例は、飲酒歴のある100人と飲酒歴のない200人を対象に、10年後にがんに罹患したかどうかを調べた結果です。このような前向き研究の場合、リスク要因以外の条件を統制しておけば、リスク要因を抱えている人(飲酒歴のある群)と、抱えていない人(飲酒歴のない群)の発症率の比(リスク比、相対リスク)から、10年後がんに罹患するリスク要因(この場合飲酒歴)の影響を評価することができます。飲酒歴のある群におけるがんの罹患するリスクは ![]() であり、飲酒歴のない群におけるがんに罹患するリスクは
であり、飲酒歴のない群におけるがんに罹患するリスクは ![]() です。これらの結果よりリスク比は
です。これらの結果よりリスク比は ![]() となり、飲酒歴のある人ががんに罹患するリスクは飲酒歴のない人に対して4倍であるということができます。
となり、飲酒歴のある人ががんに罹患するリスクは飲酒歴のない人に対して4倍であるということができます。
次に、後ろ向き研究の例について考えてみます。
| がんの罹患あり | がんの罹患なし | 合計 | |
|---|---|---|---|
| 飲酒あり | 70 | 130 | 200 |
| 飲酒なし | 30 | 150 | 180 |
| 合計 | 100 | 280 | 380 |
この例は、がんに罹患した100人とがんに罹患していない280人を対象に、これまでに飲酒歴があったかどうかを調べた結果です。このような後ろ向き研究の場合、リスク要因を抱えていた人(飲酒歴のある群)と、抱えていなかった人(飲酒歴のない群)のがんの罹りやすさ(オッズ)の比(オッズ比)から、2群間でのがんの罹りやすさを比較することができます。飲酒歴のある群におけるがんに罹患するオッズは ![]() であり、飲酒歴のない群におけるがんに罹患するオッズは
であり、飲酒歴のない群におけるがんに罹患するオッズは ![]() です。これらの結果よりオッズ比は
です。これらの結果よりオッズ比は ![]() となり、飲酒歴のない群と比べて飲酒歴のある群におけるがんの罹りやすさは2.33倍であるということができます。
となり、飲酒歴のない群と比べて飲酒歴のある群におけるがんの罹りやすさは2.33倍であるということができます。
ここで「後ろ向き研究ではなぜリスク比ではなくオッズ比を使うのか?」という疑問が浮かぶかもしれません。
後ろ向き研究例からリスクを算出しようとすると、飲酒歴のある群におけるがんに罹患するリスクは ![]() となります。しかし、飲酒歴のある群においてがんの罹患あり70人と罹患なし130人のそれぞれの人数は、200人をランダムに抽出した場合の人数とは異なります。後ろ向き研究ではがんの罹患ありと罹患なしの人数がそれぞれ100人と280人になるように調査しており、この制約が効いているために飲酒歴のある群においてがんの罹患ありと罹患なしのそれぞれの人数が70人と130人になっているに過ぎません。したがって、前向き研究のようにリスク比を算出することができないのです。
となります。しかし、飲酒歴のある群においてがんの罹患あり70人と罹患なし130人のそれぞれの人数は、200人をランダムに抽出した場合の人数とは異なります。後ろ向き研究ではがんの罹患ありと罹患なしの人数がそれぞれ100人と280人になるように調査しており、この制約が効いているために飲酒歴のある群においてがんの罹患ありと罹患なしのそれぞれの人数が70人と130人になっているに過ぎません。したがって、前向き研究のようにリスク比を算出することができないのです。
後ろ向き研究の例をもう少し詳しく見てみます。
| がんの罹患あり | がんの罹患なし | 合計 | |
|---|---|---|---|
| 飲酒あり | 70 | 130 | 200 |
| 飲酒なし | 30 | 150 | 180 |
| 合計 | 100 | 280 | 380 |
この例では、リスク比とオッズ比は次のようになります。
- リスク比:
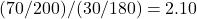
- オッズ比:
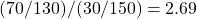
次に、「がんの罹患あり」群の数を2倍にしてみます。
| がんの罹患あり | がんの罹患なし | 合計 | |
|---|---|---|---|
| 飲酒あり | 140 | 130 | 270 |
| 飲酒なし | 60 | 150 | 210 |
| 合計 | 200 | 280 | 480 |
この例では、リスク比とオッズ比は次のようになります。
- リスク比:
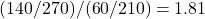
- オッズ比:
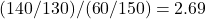
このように、後ろ向き研究の各群の人数を変えた場合、リスク比はそれにともなって変化してしまいますが、オッズ比は変わりません。そのため後ろ向き研究では、リスク比ではなく各群の人数が変わっても変化しないオッズ比を使って群間の評価を行います。







