- Step2. 中級編
- 1. 2×2のクロス集計表と様々な比率
1-5. マクネマー検定
マクネマー検定は、対応のある ![]() ペアの2値データを用いて2つの処理あるいは2つの調査の結果に差があるかどうかを検定する場合に使います。25-5章で学んだ独立性の検定と同じように2×2のクロス集計表から計算を行いますが、"対応があるデータ"の場合には独立性の検定を使うことはできない点に注意が必要です。
ペアの2値データを用いて2つの処理あるいは2つの調査の結果に差があるかどうかを検定する場合に使います。25-5章で学んだ独立性の検定と同じように2×2のクロス集計表から計算を行いますが、"対応があるデータ"の場合には独立性の検定を使うことはできない点に注意が必要です。
例えば、2つの処理を ![]() 、
、![]() とし、それぞれの反応を
とし、それぞれの反応を ![]() 、
、![]() および
および ![]() 、
、![]() としたクロス集計表の場合、
としたクロス集計表の場合、
| y1 | y2 | 合計 | |
|---|---|---|---|
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 合計 | a+c | b+d | n |
次の式で表されるカイ二乗値が自由度1のカイ二乗分布に従うことを利用して、2つの結果に差があるかを検定します。
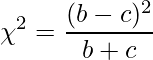
サンプルサイズが小さい場合には、次の式で示すようにイェーツの補正を行ったカイ二乗値を用いる場合もあります。
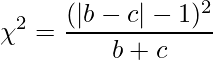
■2つの処理における割合の差の信頼区間
処理 ![]() における
における ![]() の割合は
の割合は ![]() 、処理
、処理 ![]() における
における ![]() の割合は
の割合は ![]() と表すことができます。これらの差は
と表すことができます。これらの差は
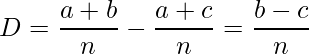
となります。この差 ![]() の信頼区間は次の式から計算することができます。
の信頼区間は次の式から計算することができます。
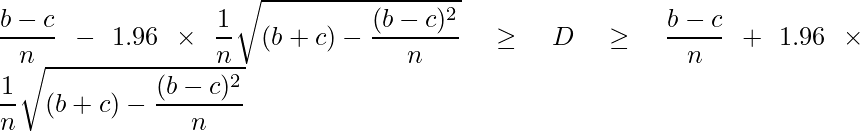
例題:
あるサプリは、寝る前に飲むことでスッキリとした目覚めをもたらしてくれることが知られています。この効果を確かめるため、ランダムに選んだ成人20人にこのサプリを飲んでもらい、目覚めに対する効果を調査しました。次の表はサプリを飲む前と飲んだ後で翌朝の目覚めがスッキリしていたかどうかを調べた結果です。ここでは、目覚めが良かったと感じた場合を○、目覚めが悪かったと感じた場合を×としています。
この結果を使って、サプリによる目覚めの効果を検証し、結論を導き出してください。有意水準を5%とします。
| No. | 飲む前 | 飲んだ後 |
|---|---|---|
| 1 | ○ | ○ |
| 2 | × | × |
| 3 | × | ○ |
| 4 | ○ | ○ |
| 5 | × | × |
| 6 | ○ | ○ |
| 7 | × | ○ |
| 8 | × | × |
| 9 | × | ○ |
| 10 | ○ | ○ |
| 11 | × | ○ |
| 12 | × | × |
| 13 | × | ○ |
| 14 | × | ○ |
| 15 | × | ○ |
| 16 | ○ | ○ |
| 17 | × | ○ |
| 18 | × | ○ |
| 19 | × | ○ |
| 20 | ○ | × |
まず、この表の結果から集計表を作成します。
| サプリ摂取後:目覚めが良い | サプリ摂取後:目覚めが悪い | 合計 | |
|---|---|---|---|
| サプリ摂取前:目覚めが良い | 5 | 1 | 6 |
| サプリ摂取前:目覚めが悪い | 10 | 4 | 14 |
| 合計 | 15 | 5 | 20 |
次にカイ二乗値を計算します。この問題ではサンプルサイズが小さいので、イェーツの補正を行ったカイ二乗値を計算します。
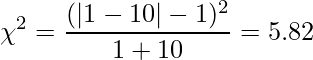
この ![]() は自由度1のカイ二乗分布に従います。統計数値表から
は自由度1のカイ二乗分布に従います。統計数値表から![]() の値を読み取ると「3.841」となっています。
の値を読み取ると「3.841」となっています。
| v | 0.99 | 0.975 | 0.95 | 0.9 | 0.1 | 0.05 | 0.025 | 0.01 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.001 | 0.004 | 0.016 | 2.706 | 3.841 | 5.024 | 6.635 |
| 2 | 0.020 | 0.051 | 0.103 | 0.211 | 4.605 | 5.991 | 7.378 | 9.210 |
| 3 | 0.115 | 0.216 | 0.352 | 0.584 | 6.251 | 7.815 | 9.348 | 11.345 |
| 4 | 0.297 | 0.484 | 0.711 | 1.064 | 7.779 | 9.488 | 11.143 | 13.277 |
| 5 | 0.554 | 0.831 | 1.145 | 1.610 | 9.236 | 11.070 | 12.833 | 15.086 |
したがって、「サプリによってもたらされる目覚めの効果は、サプリを飲まなかった場合と比べて有意な差がある」と結論づけられます。







