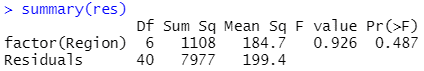- Step3. 実践編
- 2. 推定と検定
2-5. 一元配置分散分析
次のデータは、「Step1. 基礎編 29-2. 一元配置分散分析の流れ1」で用いたデータです。このデータを使って、地方によって映画館の数の母平均に差があるかを検定してみましょう。
ファイルのダウンロードはこちらから
- (日本語)one_way_ANOVA.csv
- (英語)one_way_ANOVA_eng.csv
■Excelによる解析例
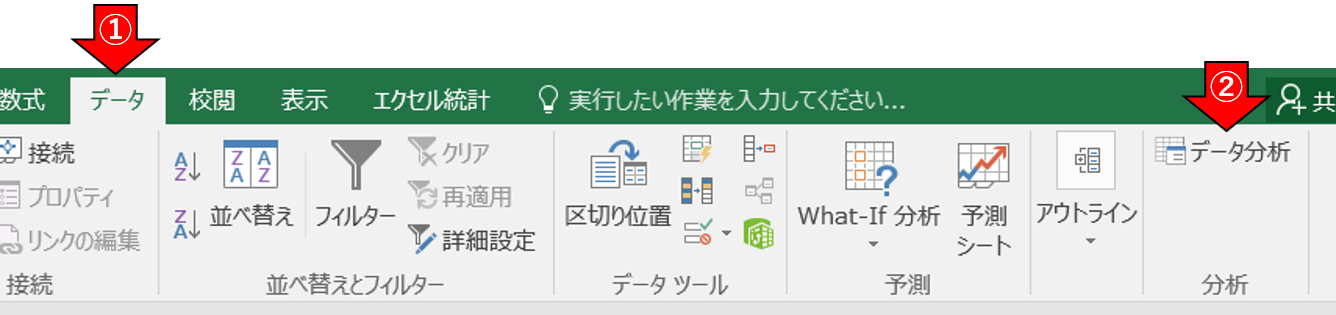
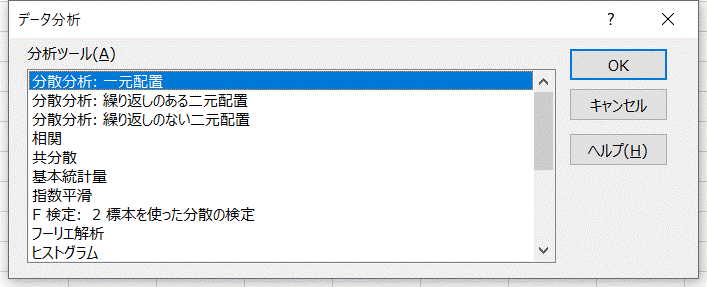
- データ > データ分析 > 分散分析: 一元配置を選択 > [OK]をクリック
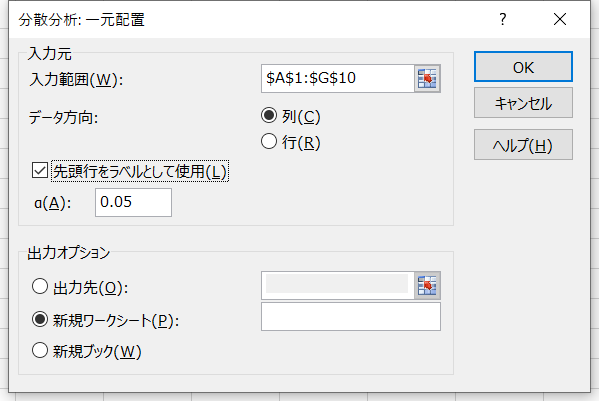
- 「入力元」と「出力オプション」を図のように設定
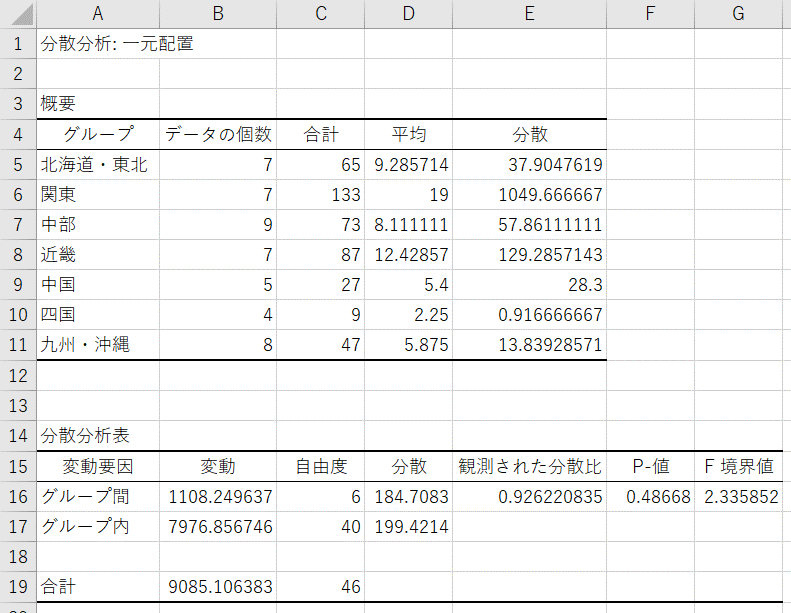
- 一元配置分散分析の結果が出力される
※「データ分析」が見当たらない方はこちらを参考に設定を行ってください。
※この結果を見ると、P=0.487であることから、地方によって映画館の数の母平均に差があるとは言えないと結論付けられます。
■Rによる解析例
dat <- read.csv("one_way_ANOVA_eng.csv", header=T) #データの読み込み
#一元配置分散分析
res <- aov(Theater ~ factor(Region), data = dat) #Region間のTheater数を比較
summary(res)
#Tukey法(Tukey-Kramer法)による多重比較
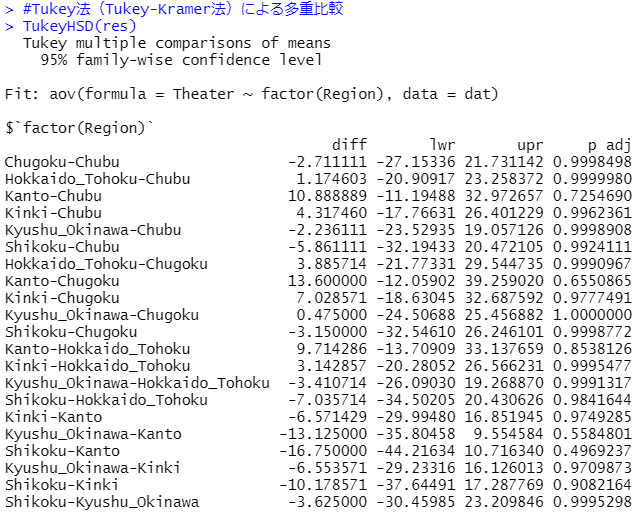
TukeyHSD(res)
#Bonferroni法による多重比較
pairwise.t.test(dat$Theater, dat$Region, p.adjust.method="bonferroni")
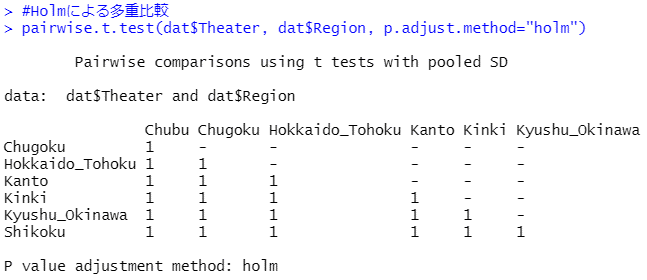
#Holm法による多重比較
pairwise.t.test(dat$Theater, dat$Region, p.adjust.method="holm")
※「p adj」はTukey法によって計算されたP値を表します。
※「Bonferroni法」と「Holm法」で計算されたP値は行列として出力されます。
■Pythonによる解析例
import pandas as pd
import pingouin as pg
dat = pd.read_csv("one_way_ANOVA_eng.csv") #データの読み込み
#一元配置分散分析
pg.anova(dv='Theater', between='Region', data=dat, detailed=True) #Region間のTheater数を比較
#Tukey法(Tukey-Kramer法)による多重比較
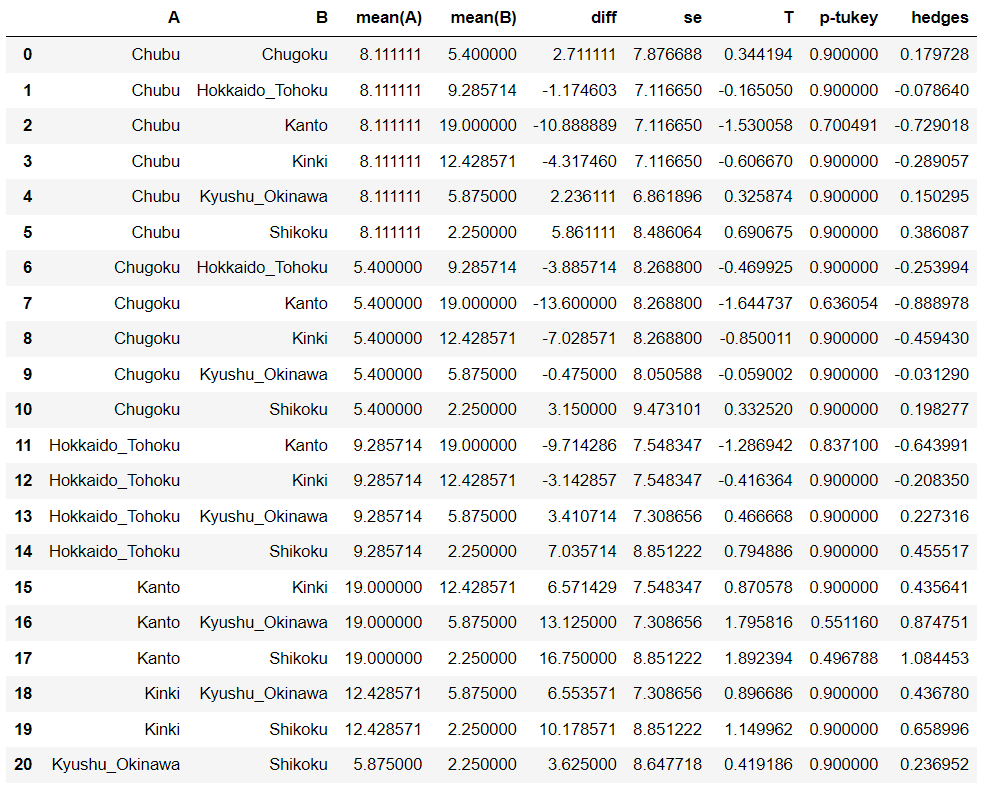
pg.pairwise_tukey(dv='Theater', between='Region', data=dat)
#Bonferroni法による多重比較
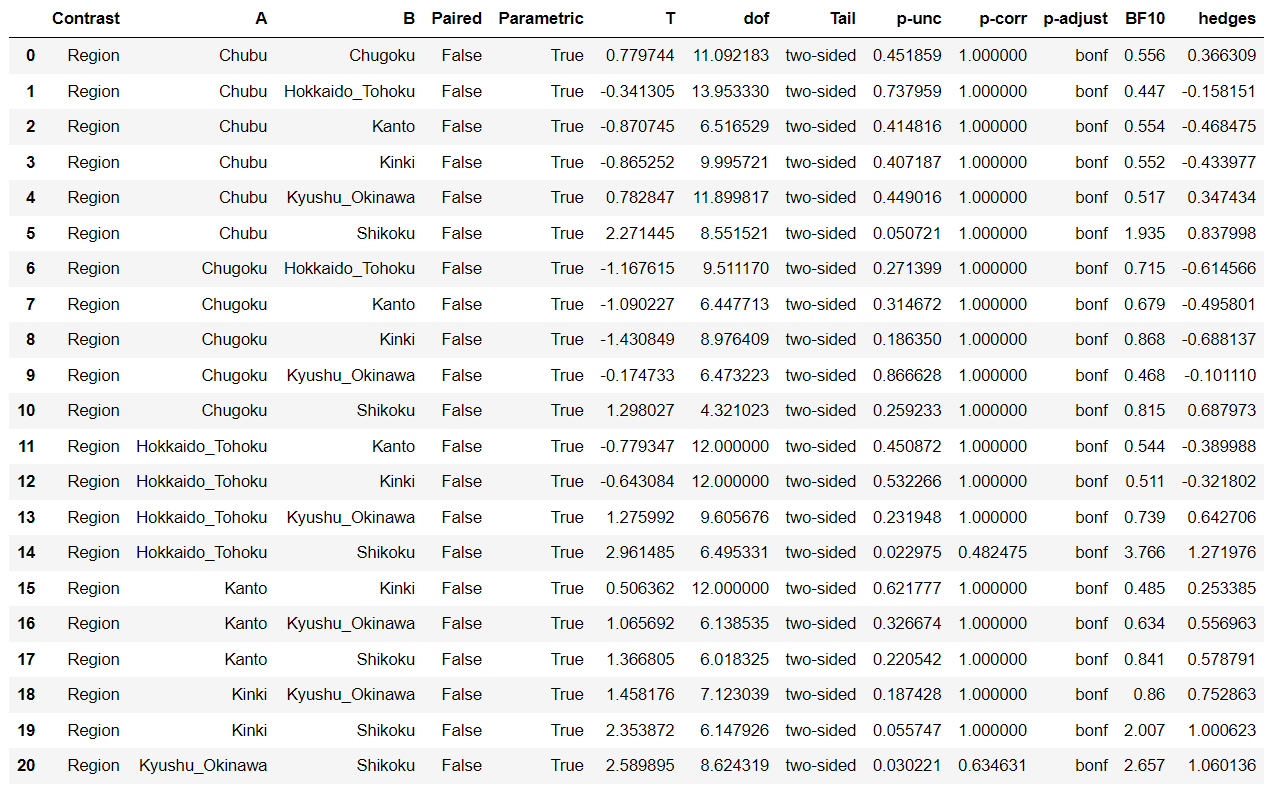
pg.pairwise_ttests(dv='Theater', between='Region', data=dat, padjust='bonf')
#Holm法による多重比較
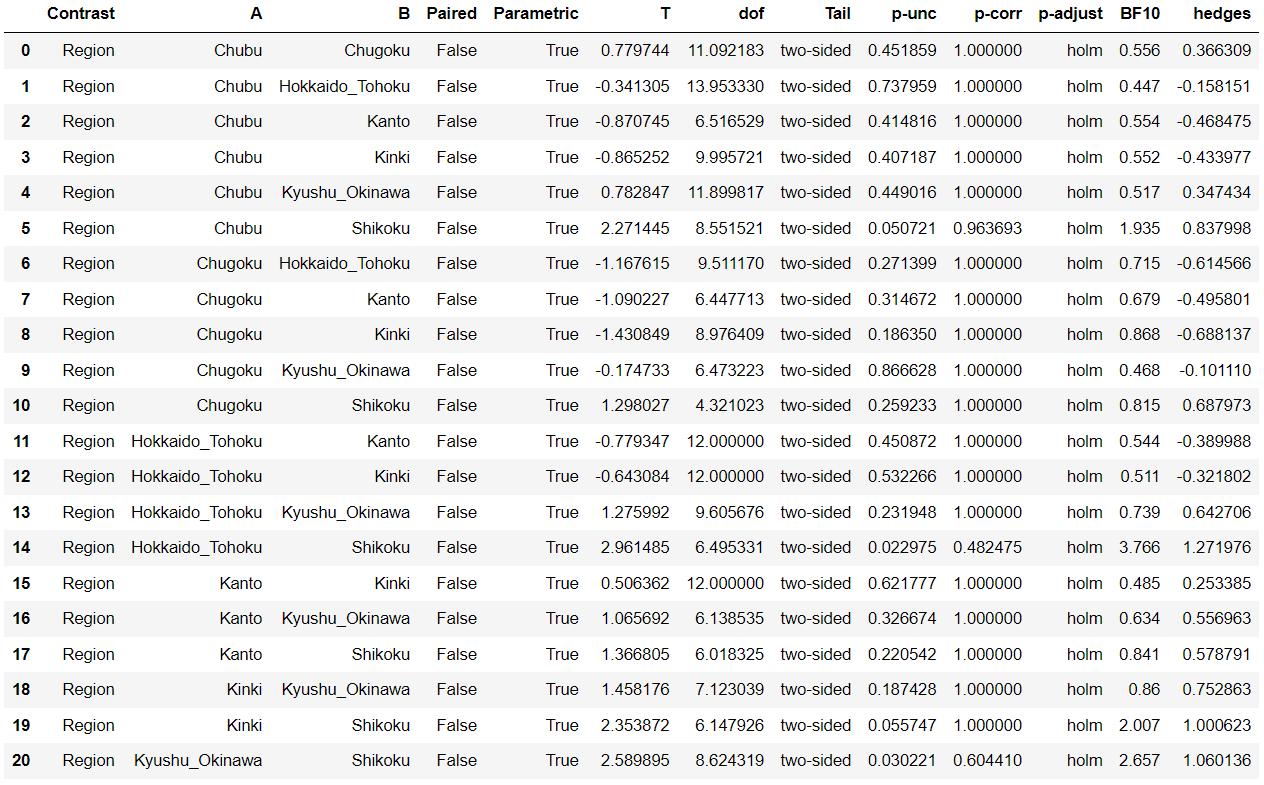
pg.pairwise_ttests(dv='Theater', between='Region', data=dat, padjust='holm')
※「p-unc (uncorrected P-value)」は補正前のP値を、「np2 (partial eta-squared)」は効果量の1つである偏イータ二乗を表します。
※「p-tukey」はTukey法によって計算されたP値を、「hedges」は効果量の1つであるヘッジズの効果量を表します。
※「p-corr」はBonferroni法によって計算されたP値を、「BF10」はベイズファクターを表します。