- Step2. 中級編
- 3. 離散型確率分布
3-2. ポアソン分布
ポアソン分布とは、二項分布において![]() が非常に大きく
が非常に大きく![]() が極めてまれな現象であるときに従う確率分布のことです。単位時間あたりにある事象が平均して
が極めてまれな現象であるときに従う確率分布のことです。単位時間あたりにある事象が平均して![]() 回起こる場合に、その事象が
回起こる場合に、その事象が![]() 回起こる確率は次の式から計算できます。
回起こる確率は次の式から計算できます。
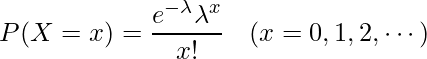
この式からポアソン分布![]() の期待値を求めてみます。
の期待値を求めてみます。
■期待値の算出
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X] &=& \sum^{\infty}_{i=0} x \times P(X=i) \\ &=& \sum_{x=0}^{\infty} x \times \frac{e^{-\lambda} \lambda^{x}}{x!} \\ &=& \sum_{x=1}^{\infty} x \times \frac{1}{x} \times \frac{e^{-\lambda} \lambda^{x}}{(x-1)!} \\ &=& \sum_{x=1}^{\infty} \frac{e^{-\lambda} \lambda^{x}}{(x-1)!} \\ &=& \sum_{x=1}^{\infty} \lambda \times \frac{e^{-\lambda} \lambda^{x-1}}{(x-1)!} \\ &=& \lambda \sum_{x=1}^{\infty} \frac{e^{-\lambda} \lambda^{x-1}}{(x-1)!} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-4f85ccfb973ea440a2c4b1af7653d7ba_l3.png)
ここで、![]() とおくと
とおくと
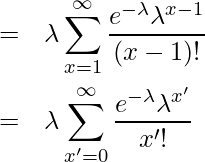
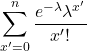 はポアソン分布の確率の総和であることから「1」になります。したがって、
はポアソン分布の確率の総和であることから「1」になります。したがって、
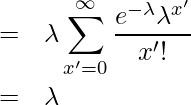
となります。
■分散の算出
分散を求めるには、![]() を使います。まず
を使います。まず![]() を求めます。
を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[X^2] &=& \sum^{\infty}_{i=1} x^2 \times P(X=i) \\ &=& \sum_{x=0}^{\infty} x^2 \times \frac{e^{-\lambda} \lambda^{x}}{x!} \\ &=& \sum_{x=0}^{\infty} (x^2-x+x) \times \frac{e^{-\lambda} \lambda^{x}}{x!} \\ &=& \sum_{x=0}^{\infty} (x^2-x) \times \frac{e^{-\lambda} \lambda^{x}}{x!} + \sum_{x=0}^{\infty} x \times \frac{e^{-\lambda} \lambda^{x}}{x!}\\ &=& \sum_{x=0}^{\infty} x(x-1) \times \frac{e^{-\lambda} \lambda^{x}}{x \times (x-1) \times (x-2)!} + \sum_{x=0}^{\infty} x \times \frac{e^{-\lambda} \lambda^{x}}{x!}\\ &=& \sum_{x=2}^{\infty} \frac{e^{-\lambda} \lambda^{x}}{(x-2)!} + \sum_{x=0}^{\infty} x \times \frac{e^{-\lambda} \lambda^{x}}{x!}\\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-dd9eb4dfeb3649b7e8418108767c5fdd_l3.png)
ここで、![]() は期待値の算出式から
は期待値の算出式から![]() となります。
となります。
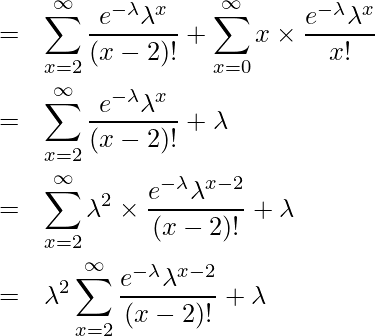
![]() はポアソン分布の確率の総和であることから「1」になります。したがって、
はポアソン分布の確率の総和であることから「1」になります。したがって、
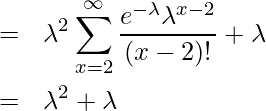
となります。次に![]() を求めます。
を求めます。
これらを使って分散![]() を求めると、
を求めると、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle V[X] &=& E[X^2] - \left\{E[X] \right\}^2 \\ &=& \lambda^{2} + \lambda - \lambda^2 \\ &=& \lambda \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-dbe493c9f119b95520013d319eec084b_l3.png)
となります。
■モーメント母関数を用いた期待値の算出
2-1章で学んだモーメント母関数を使って期待値を算出してみます。まずはじめにポアソン分布のモーメント母関数を求めます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle M_X(t) &=& E[e^{tX}] \\ &=& \sum_{x}{e^{tx}f(x)} \\ &=& \sum_{x}{e^{tx} \times \frac{e^{-\lambda} \lambda^{x}}{x!}} \\ &=& \sum_{x}{\frac{e^{tx} \times e^{-\lambda} \times \lambda^{x}}{x!}} \\ &=& e^{-\lambda} \times \sum_{x}{\frac{(e^{t} \times \lambda)^{x}}{x!}} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-5824288697ccc334e853769a58275f53_l3.png)
![]() のマクローリン展開の公式より
のマクローリン展開の公式より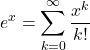 であることから
であることから
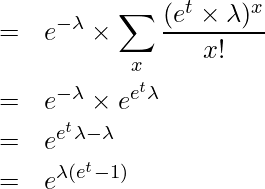
となります。2-1章で学んだように
であることから、まず![]() をtで1回微分します。
をtで1回微分します。
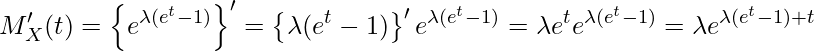
0を代入すると
となります。
■モーメントを用いた分散の算出
2-1章で学んだように
であることから、![]() をtで2回微分します。
をtで2回微分します。
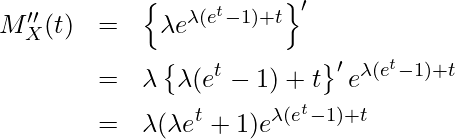
0を代入すると
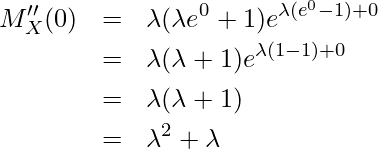
となることから、V[X]は次のように計算できます。
![]()






