- Step1. 基礎編
- 2. 度数分布とヒストグラム
2-4. ローレンツ曲線
各都道府県内にある映画館のスクリーン数のデータから下のような度数分布表を作成したところ、スクリーン数の合計が0以上100未満の都道府県は全体の約80%を占めていることが分かりました。つまり、残りの20%の都道府県には100以上のスクリーンがあり、どうやら都道府県ごとのスクリーン数の分布は「偏っている」ように思えます。
| 階級 | 階級値 | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 0以上50未満 | 25 | 24 | 0.5106 | 0.5106 |
| 50以上100未満 | 75 | 14 | 0.2979 | 0.8085 |
| ︙ | ︙ | ︙ | ︙ | ︙ |
| 合計 | - | 47 | 1.0000 | - |
この「偏り=不均等さ」を表すための曲線を「ローレンツ曲線」といいます。ローレンツ曲線を作るためには2つの累積相対度数が必要です。1つ目は各階級の度数の累積相対度数です。これは2-1章で求めた、次の度数分布表の網掛け内の値になります。
| 階級 | 階級値 | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 0以上50未満 | 25 | 24 | 0.5106 | 0.5106 |
| 50以上100未満 | 75 | 14 | 0.2979 | 0.8085 |
| 100以上150未満 | 125 | 2 | 0.0426 | 0.8511 |
| 150以上200未満 | 175 | 2 | 0.0426 | 0.8936 |
| 200以上250未満 | 225 | 3 | 0.0638 | 0.9574 |
| 250以上300未満 | 275 | 1 | 0.0213 | 0.9787 |
| 300以上350未満 | 325 | 0 | 0.0000 | 0.9787 |
| 350以上400未満 | 375 | 1 | 0.0213 | 1.0000 |
| 合計 | - | 47 | 1.0000 | - |
2つ目は、各階級に属する値の合計の累積相対度数です。例えば、階級「50以上100未満」のスクリーン数の累積相対度数は、以下の手順で求められます。
- (1) 47都道府県すべてがもつスクリーン数の合計:
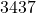
- (2) 「0以上50未満」の階級に属する24の都道府県内にあるスクリーン数の合計:
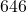
- (3) 「0以上50未満」の階級に属する24の都道府県内にあるスクリーン数の相対度数:
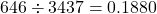
- (4) 「50以上100未満」の階級に属する14の都道府県内にあるスクリーン数の合計:
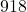
- (5) 「50以上100未満」の階級に属する14の都道府県内にあるスクリーン数の相対度数:
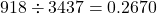
したがって、スクリーン数の合計が「50以上100未満」の階級のスクリーン数の累積相対度数は![]() となります。このようにして作成した度数分布表が次の表です。
となります。このようにして作成した度数分布表が次の表です。
| 階級 | 度数 | 累積相対度数 | スクリーン数合計 | スクリーン数の 相対度数 | スクリーン数の 累積相対度数 |
|---|---|---|---|---|---|
| 0以上50未満 | 24 | 0.5106 | (2) 646 | (3) 0.1880 | 0.1880 |
| 50以上100未満 | 14 | 0.8085 | (4) 918 | (5) 0.2670 | 0.4550 |
| 100以上150未満 | 2 | 0.8511 | 239 | 0.0695 | 0.5246 |
| 150以上200未満 | 2 | 0.8936 | 377 | 0.1097 | 0.6343 |
| 200以上250未満 | 3 | 0.9574 | 641 | 0.1865 | 0.8208 |
| 250以上300未満 | 1 | 0.9787 | 258 | 0.0751 | 0.8958 |
| 300以上350未満 | 0 | 0.9787 | 0 | 0.0000 | 0.8958 |
| 350以上400未満 | 1 | 1.0000 | 358 | 0.1042 | 1.0000 |
| 合計 | 47 | - | (1) 3437 | 1.0000 | - |
この度数分布表の「累積相対度数」を横軸に、「スクリーン数の累積相対度数」を縦軸にとった折れ線グラフが都道府県ごとのスクリーン数のローレンツ曲線です。グラフ中の「完全平等線」については次の2-5章で説明します。

■おすすめ書籍
コア・テキスト統計学は経済学をベースに書かれている統計入門書なので、ローレンツ曲線やジニ係数、経済指標についての説明が比較的充実しています。
2. 度数分布とヒストグラム
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 2. 度数分布とヒストグラム
2-1. 度数分布と累積度数分布







