29. 一元配置分散分析

練習問題（29. 一元配置分散分析）

一元配置分散分析の帰無仮説のうち、正しいものを次の選択肢の中から選べ。

全ての群の母平均は等しい
全ての群の母平均は等しくない
全ての群のうち、いくつかの群の母平均は等しい
全ての群のうち、いくつかの群の母平均は等しくない

答えを見る

答え閉じる: a群の母平均を 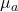$\mu_a$ とすると、分散分析の帰無仮説は「 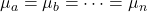$\mu_a = \mu_b = \cdots =\mu_n$ 」です。これは「すべての群の母平均が等しい」ことを意味しています。したがって、答えは「1」となります。

分散分析の結果が有意であったとき、どのように解釈するのが正しいか。次の選択肢の中から選べ。

全ての群の母平均は等しい
全ての群の母平均は互いに異なる
全ての群のうち母平均が異なる群があるが、それがどの群かは分からない
母平均が異なる群が存在し、それを特定できる

答えを見る

答え閉じる

分散分析の帰無仮説「全ての群の母平均が等しい」が棄却された場合、「どこかの群で母平均が異なる」と解釈します。しかし、具体的に「どの群の母平均が異なるか」については分からないことに注意する必要があります。

したがって、答えは「3」となります。

次の分散分析表の空欄AからDを埋めよ。

因子	平方和	自由度	平均平方	F　値
要因	3000	10	A	B
残差	C	60	D
全体	7500	70

答えを見る

答え閉じる

分散分析表は、次のようなルールに従って計算できます。

全体の平方和＝要因の平方和+残差の平方和
全体の自由度＝要因の自由度+残差の自由度
平均平方＝平方和÷自由度
F値＝要因の平均平方÷残差の平均平方

これらのルールを利用すると、分散分析表を埋めることができます。まず、Aについては3.より「要因の平均平方＝要因の平方和÷要因の自由度」で計算できます。この式に数値をあてはめると、3000÷10＝300と求められます。

Cについては、1.より「7500＝3000+残差の平方和」から、Cは4500と計算できます。Dは、C=4500と自由度が60であることから、Aと同様にして4500÷60＝75と計算できます。

最後に、4.を用いて、F値＝300÷75、つまりB=4と計算できます。まとめると、「A=300　B=4　C=4500　D=75」が答えとなります。

9匹のマウスをランダムに3つの群に分け、3種類の薬剤を投与した後にある臓器の重量（g）を測定したところ、下の表の結果を得た。薬剤による臓器の重量の平均値に差があるかどうかを有意水準0.05で検定せよ。

薬剤A	薬剤B	薬剤C
2.51	3.71	3.67
3.06	3.62	3.75
3.19	3.46	3.90

このような問題のように、2つ以上の群の平均値を比較したい時には分散分析を行います。分散分析を行うためには下の「分散分析表」を完成させる必要があります。

因子	平方和	自由度	平均平方	F　値
要因	⑤	⑦	⑨	⑪
残差	0.32	6	⑩
全体	⑥	⑧

分散分析のポイントは全体の平均値から各群の平均値がどのくらいずれているかを見ることです。

全体の平均値は(①　　　　　)です。また、各群の平均値はA群が(②　　　　　)、B群が(③　　　　　)、C群が(④　　　　　)になります。

分散分析では「平均値のズレ」を「平方和」で見ます。平方和は「ズレ」を2乗したものをすべて足したものになります。まずは因子（薬剤）の平方和を計算します。これは、因子（薬剤）によって平均がどれくらいずれているかを表す平方和です。各郡のデータは3つずつあるので、式は3×(②-①)²+3×(③-①)²+3×(④-①)²となり、計算すると(⑤　　　　　)となります。

次に全体の平方和を計算します。これは、個々のデータの値が全体の平均からどのくらいずれているかを表す平方和です。式は(2.51-①)²+(3.71-①)²+(3.67-①)²+(3.06-①)²+(3.62-①)²+(3.75-①)²+(3.19-①)²+(3.46-①)²+(3.90-①)² となり、計算すると(⑥　　　　　)となります。残差の平方和は全体の平方和から因子（薬剤）の平方和を引いたもので、⑥から⑤を引いた値になります。

ここからは自由度を求めます。因子（薬剤）の自由度は比較する群の数から1を引いたものなので、(⑦　　　　　)です。また、全体の自由度は比較するデータの個数から1を引いたものなので(⑧　　　　　)です。残差の自由度は全体の自由度から因子（薬剤）の自由度を引いたもので、⑧から⑦を引いた値になります。

平方和と自由度が求められたあとは、平均平方を求めます。これは、平方和を自由度で割ったものです。⑨であれば⑤を⑦で割ったもの(⑨　　　　　)、⑩であれば0.32を6で割ったもの(⑩　　　　　)になります。全体の平均平方は求める必要はありません。

ここまでで、「全体のズレ」を「因子（薬剤）のズレ」と「残差によるズレ（それ以外のズレ）」の2つに分けることができました。最後に「因子（薬剤）のズレ（一番知りたいもの）」が「残差によるズレ」と比較してどのくらい大きいのかを調べるために、⑨と⑩を使ってF検定を行います。F値は⑨を⑩で割ることで求められ、(⑪　　　　　)になります。

答えを見る

答え閉じる

全体の平均値は(①3.43　　)です。また、各群の平均値はA群が(②2.92　　)、B群が(③3.60　　)、C群が(④3.77　　)になります。分散分析表を完成させると次のようになります。

因子	平方和	自由度	平均平方	F　値
要因	⑤1.21	⑦2	⑨0.61	⑪12.2
残差	0.33	6	⑩0.055
全体	⑥1.54	⑧8

練習問題4で完成させた分散分析表を用いて、薬剤によるマウスの臓器の重量の平均値に差があるかどうかを有意水準0.05で検定せよ。

答えを見る

答え閉じる

有意水準5%では、F分布表を読み取ると自由度(2, 6)のF値は5.14です。今回の分散分析表から求められたF値は⑪12.2なので帰無仮説は棄却されます。つまり、各群の母平均に差があるといえます。

分散分析では、残差のばらつき（それ以外のズレ）に対する要因のばらつき（全体の平均値からの因子の各水準の平均値のズレ）が相対的に大きいかどうかを検定します。大きい場合には要因による効果は有意であると判断されますが、小さい場合には要因による効果は有意であるとはいえません。つまり、要因のばらつきが相対的に大きいかどうかだけを見ればよいので、分散分析では必ず「片側検定」を行います。