次のデータは、「Step1. 基礎編　27-1. 単回帰分析」で用いたデータです。このデータを使って、薬局の数（y）を目的変数、人口密度（x）を説明変数とする単回帰式を求めてみましょう。

ファイルのダウンロードはこちらから

• （日本語）linear_regression1.csv
• （英語）linear_regression1_eng.csv

■Excelによる解析例

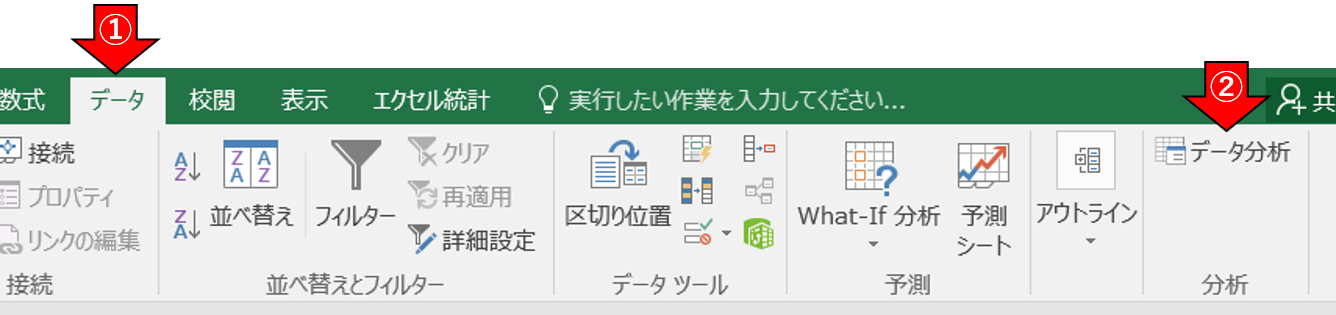
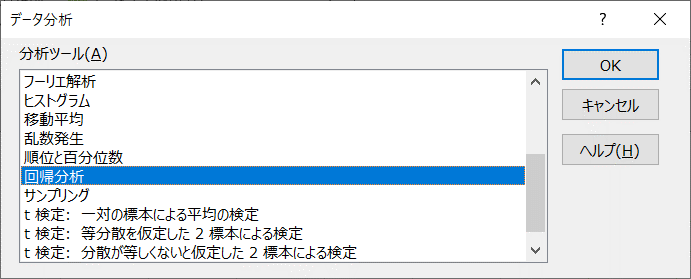
1. データ > データ分析 > 回帰分析を選択 > [OK]をクリック

※「データ分析」が見当たらない方はこちらを参考に設定を行ってください。



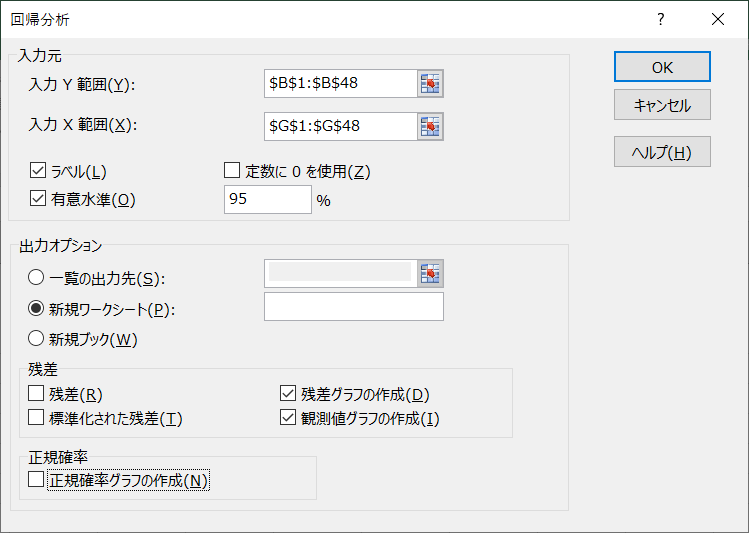
2. 「入力元」と「出力オプション」を図のように設定

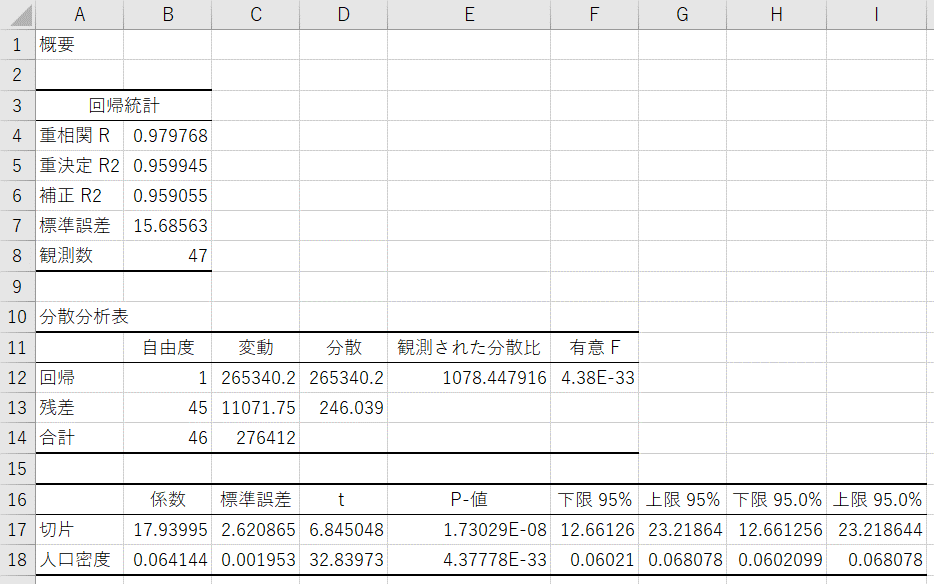
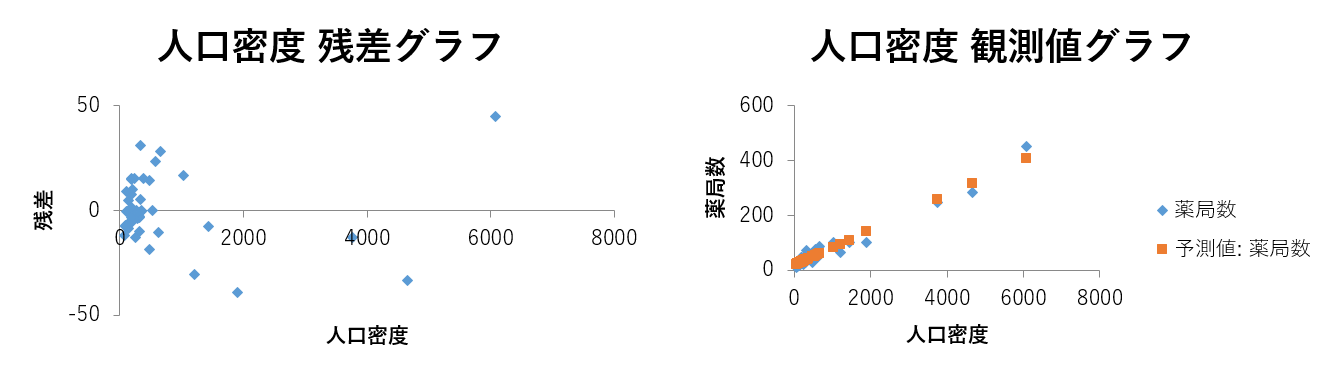
3. 回帰分析の結果が出力される

※この結果を見ると、推定された単回帰式はであることが分かります。

■Rによる解析例

dat <- read.csv("linear_regression1_eng.csv", header=T, row.names=1)  #データの読み込み

#線形回帰
res <- lm(formula = Pharmacy ~ Pop_density, data = dat)  #Pharmacyをy、Pop_Densityをx、読み込むデータをdatとして線形回帰を行う
summary(res)  #線形回帰の結果を表示

#回帰直線のプロット
plot(x = dat$Pop_density, y = dat$Pharmacy, xlab = "Population density", ylab = "Pharmacy")  #datのPop_densityとPharmacyの値をプロット
abline(res, col = "red", lwd = 2)  #回帰直線を重ねる

#回帰診断
par(mfrow = c(2, 2))  #2x2の図を表示するように設定
plot(res)  #回帰診断の結果を表示

par(mfrow=c(1,1))  #1x1の図を表示するように設定（初期設定に戻す）

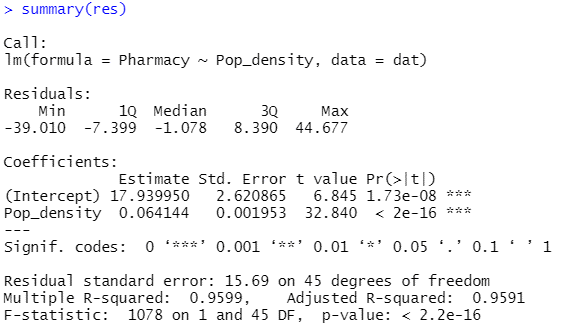
結果の見方

• Residuals：残差の分布
• Coefficients：回帰分析により推定された偏回帰係数、標準誤差、t値、P値
• Residual standard error：残差の標準誤差（ばらつき）と自由度
• Multiple R-squared：決定係数
• Adjusted R-squared：自由度調整済み決定係数
• F-statistic：回帰式の有意性の検定結果（分散分析の結果；F値、自由度、P値）

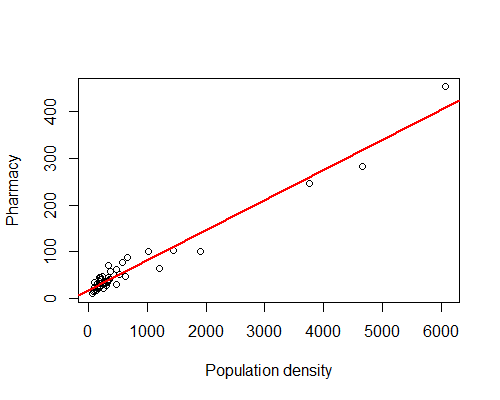
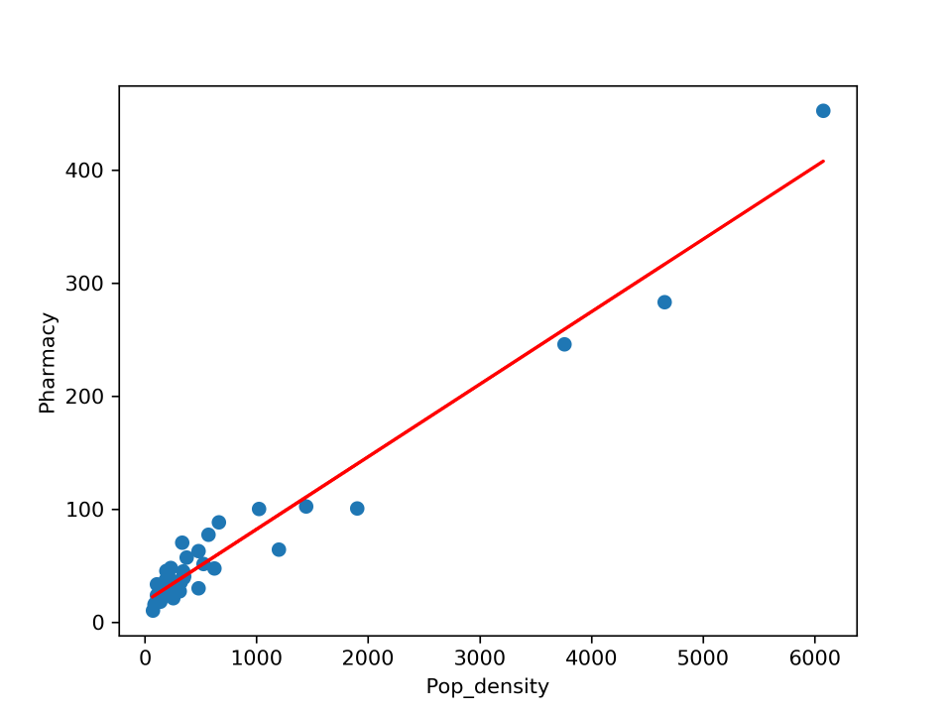
実際の値を用いた散布図上に、回帰直線を重ねた図です。回帰直線の当てはまりの良さを視覚的に確認することができます。

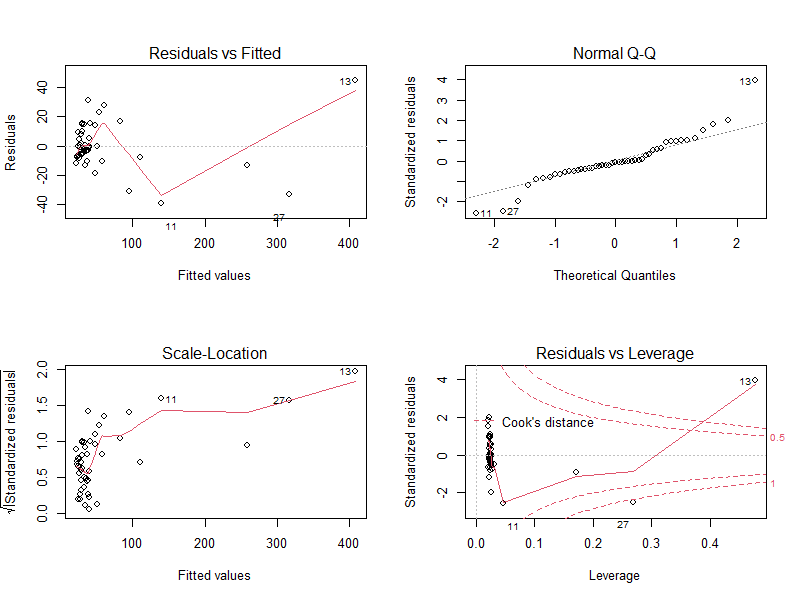
結果の見方

• Residuals vs Fitted：x軸は回帰直線により予測されたyの値、y軸は予測値と観測値との差（残差）
• Normal Q-Q：残差のQ-Qプロット（残差の正規性を確認するためのプロット）
• Scale-Location：x軸は回帰直線により予測されたyの値、y軸は標準化した残差の絶対値の平方根を取った値
• Residuals vs Leverage：Cookの距離（Cookの距離が0.5を超えると回帰式への影響が大きい＝外れ値の可能性が高い）

■Pythonによる解析例

import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm

dat = pd.read_csv("linear_regression1_eng.csv")  #データの読み込み

#線形回帰
x = dat["Pop_density"]  #Pop_densityをxとする
x2 = sm.add_constant(x)  #切片を計算するために説明変数のデータの中に全て1からなる列を追加
y = dat["Pharmacy"]  #Pharmacyをyとする
res = sm.OLS(y, x2).fit()  #y、xを用いて線形回帰を行う
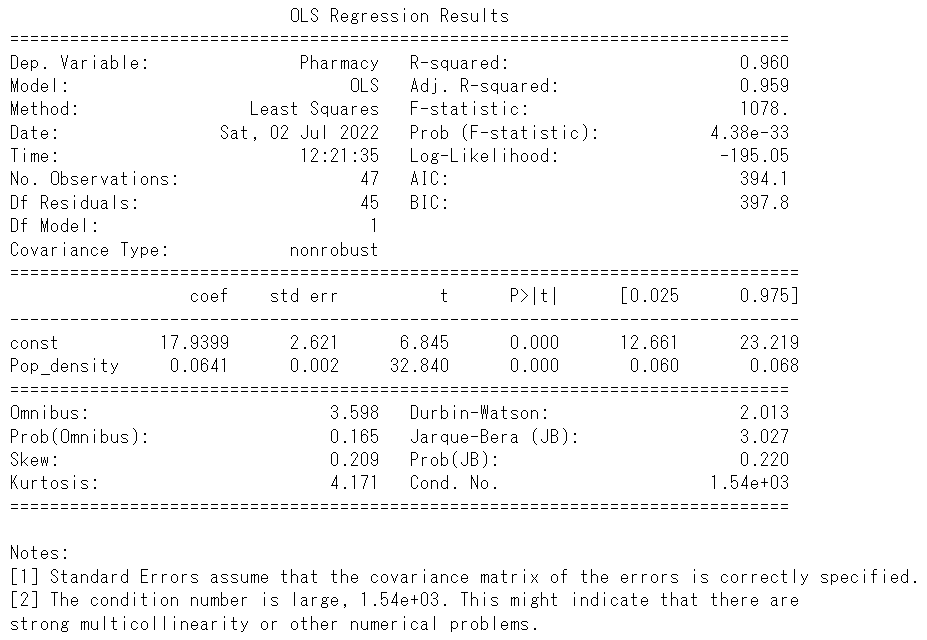
print(res.summary())  #線形回帰の結果を表示

#回帰直線のプロット
plt.plot(x, y, "o")  #datのPop_densityとPharmacyの値をプロット
plt.plot(x, res.predict(x2), color = 'red')  #回帰直線を重ねる
plt.xlabel("Pop_density")  #x軸ラベルを設定
plt.ylabel("Pharmacy")  #y軸ラベルを設定

plt.show()

#回帰診断
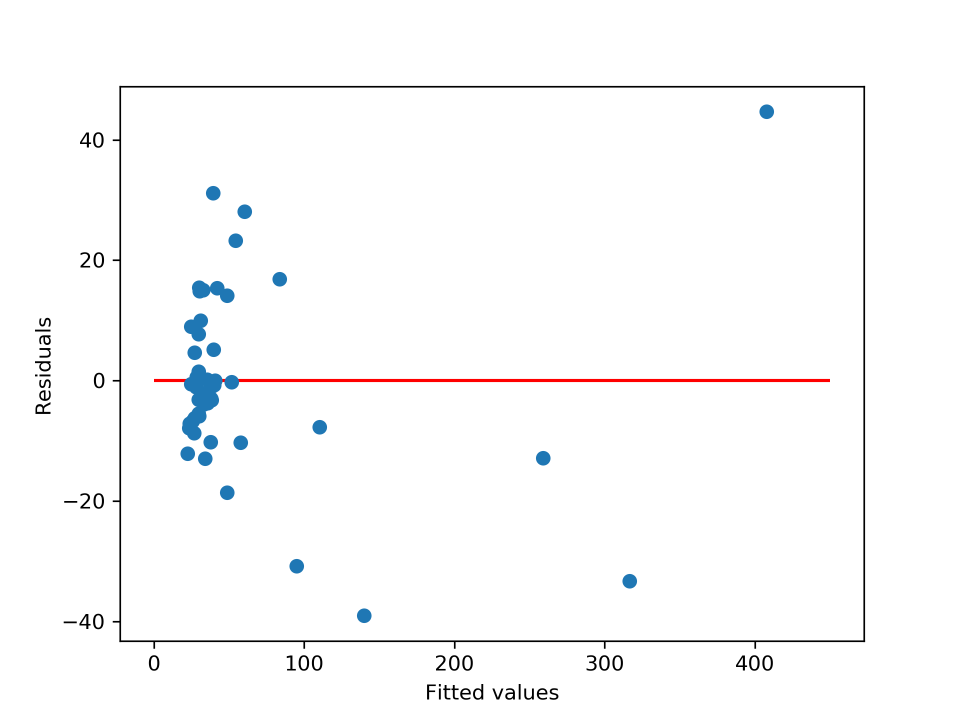
plt.plot(res.predict(x2), y- res.predict(x2), "o")  #yの予測値と残差の値をプロット    
plt.hlines(y = 0, xmin = 0, xmax = 450, color = 'red')  #y = 0の直線を重ねる
plt.xlabel('Fitted values')  #x軸ラベルを設定                           
plt.ylabel('Residuals')  #y軸ラベルを設定                                   

plt.show()

結果の見方

• R-squared：決定係数
• Adj. R-squared：自由度調整済み決定係数
• F-statistic、Prob(F-statistic)：回帰式の有意性の検定結果
• Log-Likelihood：対数尤度（対数尤度が大きいほど当てはまりが良いモデル）
• AIC：赤池情報量規準（AICが小さいほど当てはまりが良いモデル）
• BIC：ベイズ情報量基準（対数尤度が小さいほど当てはまりが良いモデル）

• Coef：回帰分析により推定された偏回帰係数
• std err：標準誤差
• t：t値
• P>|t|：P値
• [0.025、0.975]：偏回帰係数の95%信頼区間

• Omnibus、Prob(Omnibus)：残差に対する歪度と尖度によるオムニバス検定（正規性の検定の1つ）とP値
• Skew：残差の歪度
• Kurtosis：残差の尖度
• Durbin-Watson：残差間の自己相関
• Jarque-Bera(JB)、Prob(JB)：残差に対するジャーク=ベラ検定（正規性の検定の1つ）とP値
• Condo. No.：多重共線性の指標