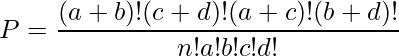- Step2. 中級編
- 5. 統計的検定
5-2. フィッシャーの正確確率検定
■独立性の検定において注意が必要な場合
独立性の検定を行う際には次の2つのケースに注意が必要です。
- 期待度数が1未満のセルがある
- 期待度数が5未満のセルが、全体のセルの20%以上ある
このような場合には、独立性の検定結果が正確ではない場合があります。例えば次のような2行×2列のクロス集計表について考えます。
| 国語が好き | 国語が嫌い | 計 | |
|---|---|---|---|
| 数学が好き | 2 | 8 | 10 |
| 数学が嫌い | 10 | 20 | 30 |
| 計 | 12 | 28 | 40 |
このクロス集計表から国語の好き嫌いと数学の好き嫌いの間に関連があるといえるかどうかを独立性の検定によって検定する場合、各セルの期待値は次のようになります。
| 国語が好き | 国語が嫌い | 計 | |
|---|---|---|---|
| 数学が好き | 3 | 7 | 10 |
| 数学が嫌い | 9 | 21 | 30 |
| 計 | 12 | 28 | 40 |
ここで、「国語が好き・数学が好き」のセルの期待値が「3」になっていることから、ケース2に当てはまります。このような場合には「フィッシャーの正確確率検定」を使って検定を行います。
■フィッシャーの正確確率検定
フィッシャーの正確確率検定は、独立性の検定と同様にクロス集計表の行要素と列要素の2つの属性が独立であるかを検定する方法です。独立性の検定のようにカイ二乗分布による近似的なP値を用いて検定を行うのではなく、起こりうるすべての組み合わせその中で観測された以上の差がつく組み合わせの確率をP値とし、検定を行います。
まず、国語の好き嫌いと数学の好き嫌いのクロス集計表を使って、起こりうるすべての組み合わせを考えます。このとき、「行の合計と列の合計を一定」とするのがポイントです。例えば、「国語が好き・数学が好きが0人」のときには次のようなクロス集計表になります。
| 国語が好き | 国語が嫌い | 計 | |
|---|---|---|---|
| 数学が好き | 0 | 10 | 10 |
| 数学が嫌い | 12 | 18 | 30 |
| 計 | 12 | 28 | 40 |
起こりうるすべての組み合わせは次のようになります。
| 国語好き/数学好き | 国語好き/数学嫌い | 国語嫌い/数学好き | 国語嫌い/数学嫌い |
|---|---|---|---|
| 0 | 12 | 10 | 18 |
| 1 | 11 | 9 | 19 |
| 2 | 10 | 8 | 20 |
| 3 | 9 | 7 | 21 |
| 4 | 8 | 6 | 22 |
| 5 | 7 | 5 | 23 |
| 6 | 6 | 4 | 24 |
| 7 | 5 | 3 | 25 |
| 8 | 4 | 2 | 26 |
| 9 | 3 | 1 | 27 |
| 10 | 2 | 0 | 28 |
次に、各組み合わせが起こる確率を求めます。「国語が好き・数学が好きが0人」のときの確率は次のように計算できます。
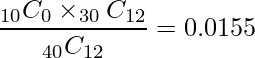
「国語が好き・数学が好きが1人」のときの確率は次のように計算できます。
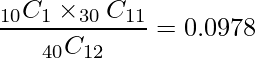
これらの結果をまとめると次のようになります。
| 国語好き/数学好き | 国語好き/数学嫌い | 国語嫌い/数学好き | 国語嫌い/数学嫌い | 確率 |
|---|---|---|---|---|
| 0 | 12 | 10 | 18 | 0.0155 |
| 1 | 11 | 9 | 19 | 0.0978 |
| 2 | 10 | 8 | 20 | 0.242 |
| 3 | 9 | 7 | 21 | 0.307 |
| 4 | 8 | 6 | 22 | 0.220 |
| 5 | 7 | 5 | 23 | 0.0918 |
| 6 | 6 | 4 | 24 | 0.0223 |
| 7 | 5 | 3 | 25 | 0.00306 |
| 8 | 4 | 2 | 26 | 2.21e-4 |
| 9 | 3 | 1 | 27 | 7.27e-6 |
| 10 | 2 | 0 | 28 | 7.79e-8 |
最後に、観測された以上の差がつく組み合わせの確率を求めます。この確率は「国語が好き・数学が好きが2人」となる確率よりも低いものをすべて足し合わせたものです。この表を見ると「国語が好き・数学が好きが3人」となる確率以外がすべて該当します。したがって、求める確率は![]() となり「有意水準5%において、帰無仮説を棄却しない」という結果になります。つまり「国語の好き嫌いと数学の好き嫌いの間に関連があるとはいえない」と結論づけられます。
となり「有意水準5%において、帰無仮説を棄却しない」という結果になります。つまり「国語の好き嫌いと数学の好き嫌いの間に関連があるとはいえない」と結論づけられます。
■フィッシャーの正確確率検定と独立性の検定のどちらを使えばよいか
検定を行うクロス集計表が上で挙げた2つのケースに当てはまる場合には、フィッシャーの正確確率検定を使ったほうが確率をより正確に計算できます。2つのケースに当てはまらない場合には、どちらの検定法を使っても問題ありません。ただし、サンプルサイズが非常に多い場合にはフィッシャーの正確確率検定は計算量が多くなるために確率の計算ができなかったり計算に時間がかかりすぎてしまう場合があります。そのような場合には独立性の検定を使うほうがよいです。
【まとめ】フィッシャーの正確確率検定におけるP値を求める方法
2行×2列のクロス集計表の各セルの値を以下のように ![]() を用いて表したとき、この組み合わせが得られる確率
を用いて表したとき、この組み合わせが得られる確率![]() は超幾何分布を用いて下式から求めることができます。
は超幾何分布を用いて下式から求めることができます。
| a | b | a+b | |
| c | d | c+d | |
| a+c | b+d | n |