- Step1. 基礎編
- 6. 分散と標準偏差
6-4. 変動係数
変動係数(Coefficient of Variation)は、標準偏差を平均値で割った値のことで、単位の異なるデータのばらつきや、平均値に対するデータとばらつきの関係を相対的に評価する際に用いる単位を持たない(=無次元の)数値です。変動係数はCVで表されることがあります。
変動係数=標準偏差÷平均値
例題1:
次の表は、あるスーパーマーケットで肉の値段を10日間調査した結果をまとめたものです。この調査の結果、鶏ささみは100gあたり平均80円、標準偏差は20円でした。一方、牛ステーキ肉は100gあたり平均1800円、標準偏差は300円でした。どちらの肉の方が値段のばらつきが大きいでしょうか。
| 肉の種類 | 平均価格(円) | 標準偏差(円) |
|---|---|---|
| 鶏ささみ | 80 | 20 |
| 牛ステーキ肉 | 1800 | 300 |
標準偏差の値をそのまま比較すると牛ステーキ肉のばらつきが大きいことが分かります。これは、牛ステーキ肉の値段が高いため、鶏ささみと比較して標準偏差の値が大きくなってしまっているためです。

このような場合に変動係数を用いると、それぞれの平均値に対する相対的なばらつきの大きさを見ることができます。
- 鶏ささみの変動係数:20÷80=0.25
- 牛ステーキ肉の変動係数:300÷1800≒0.167
変動係数を計算すると、平均値に対しては鶏ささみの値段の方が相対的にばらつきが大きいという結果になりました。
例題2:
次の表は、ある男性とあるラットの体重を10回測定した結果をまとめたものです。どちらのデータのほうが測定結果のばらつきが大きいでしょうか。
| 測定回数 | 男性の体重(kg) | ラットの体重(kg) |
|---|---|---|
| 1回目 | 59 | 0.5 |
| 2回目 | 61 | 0.4 |
| 3回目 | 59 | 0.6 |
| 4回目 | 61 | 0.3 |
| 5回目 | 59 | 0.5 |
| 6回目 | 61 | 0.44 |
| 7回目 | 61 | 0.33 |
| 8回目 | 59 | 0.4 |
| 9回目 | 61 | 0.6 |
| 10回目 | 59 | 0.35 |
| 平均 | 60 | 0.44 |
・ある男性の体重を10回測定した場合の標準偏差
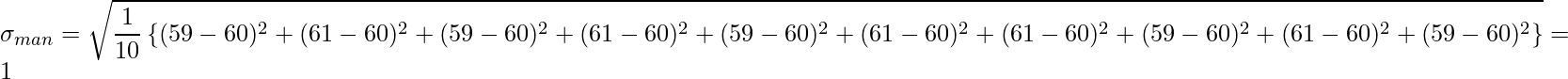
・あるラットの体重を10回測定した場合の標準偏差
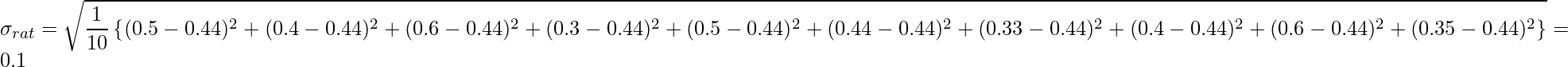
男性の体重の標準偏差は1[kg]、ラットの体重の標準偏差は0.1[kg]となりました。したがって、ラットの体重よりも男性の体重のばらつきが大きいことが分かります。

次に「変動係数」を用いて、男性の平均体重60kgとラットの平均体重0.44kgに対する相対的なばらつきの大きさを算出してみます。
- 男性の体重の変動係数:1÷60≒0.017
- ラットの体重の変動係数:0.1÷0.44≒0.227
この結果から、平均体重に対してはラットの体重の方が相対的にばらつきが大きいということが分かります。
【コラム】変動係数を使うコツ
変動係数は、平均値に対して標準偏差が比例関係にあるものに対して適用するのが正しい使い方です。すなわち、比例尺度の場合に有効な指標であり、間隔尺度では参考になりません。
この章の例題2の男性とマウスの体重の測定結果のように、平均値が大きくなればその分ばらつきも大きくなっていくようなデータに対して正しい評価を行うことができます。他にも、実験データにおける計量の正確さ比較する場合にも変動係数が用いられることがあります。変動係数が小さいほど、測定の精度が高いことを意味します。
例えば水質基準項目の測定精度の資料では、厚生労働省が示した水質基準項目の物質それぞれについて、測定精度が変動係数によって示されています。
6. 分散と標準偏差
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
記述統計量
- 1. 統計ことはじめ
1-4. 変数の尺度
- 6. 分散と標準偏差
6-2. 標準偏差
- ブログ
変数の分類







