- Step1. 基礎編
- 6. 分散と標準偏差
6-1. 分散
例題:
ある実験を行い、次の2つのデータが得られました。AもBもどちらも平均は3.5ですが、この2つのデータのばらつき具合は似ていると言えるでしょうか。
| データA | データB |
|---|---|
| 1 | 3.5 |
| 2 | 3.5 |
| 3 | 3.5 |
| 4 | 3.5 |
| 5 | 3.5 |
| 6 | 3.5 |
| 合計=21 | 合計=21 |
| 平均=3.5 | 平均=3.5 |
以下の3つの値を用いて、2つのデータの平均値からの「ばらつき具合」を比較してみます。
- 「平均値からの各データの」の平均値
- 「平均値からの各データの差の絶対値」の平均値
- 「平均値からの各データの差の2乗」の平均値
1. 「平均値からの各データの」の平均値
下の表は平均値とそれぞれのデータとの差をまとめたものです。この差の平均はデータAもデータBも0となりました。
| データA | 平均値からの差 | データB | 平均値からの差 |
|---|---|---|---|
| 1 | 2.5 | 3.5 | 0 |
| 2 | 1.5 | 3.5 | 0 |
| 3 | 0.5 | 3.5 | 0 |
| 4 | -0.5 | 3.5 | 0 |
| 5 | -1.5 | 3.5 | 0 |
| 6 | -2.5 | 3.5 | 0 |
| 合計=21 | 合計=0 | 合計=21 | 合計=0 |
| 平均=3.5 | 平均=0 | 平均=3.5 | 平均=0 |
ここで算出した「平均値と各データの差」のことを、統計学では「偏差」といいます。「平均値より大きいデータの偏差の和」と「平均値より小さいデータの偏差の和」が打ち消しあうために、偏差の和は常に「0」になります。したがって、この方法ではデータのばらつき具合を比較することはできません。
2. 「平均値からの各データの差の絶対値」の平均値
比較する値が必ず0以上となるように、平均値とそれぞれのデータとの差の絶対値の平均を考えてみます。
| データA | 平均値からの差の絶対値 | データB | 平均値からの差の絶対値 |
|---|---|---|---|
| 1 | 2.5 | 3.5 | 0 |
| 2 | 1.5 | 3.5 | 0 |
| 3 | 0.5 | 3.5 | 0 |
| 4 | 0.5 | 3.5 | 0 |
| 5 | 1.5 | 3.5 | 0 |
| 6 | 2.5 | 3.5 | 0 |
| 合計=21 | 合計=9 | 合計=21 | 合計=0 |
| 平均=3.5 | 平均(=平均偏差)=1.5 | 平均=3.5 | 平均(=平均偏差)=0 |
平均値から各データの差の絶対値の平均(=絶対値を付けた偏差の平均)はデータAの方が大きいことから、データAの方が平均値からのばらつき具合が大きいということが分かります。この値は「平均偏差」と呼ばれます。しかし、絶対値の計算は絶対値記号を外すために場合分けをする必要があり、数学的に面倒であるというデメリットがあります。
3. 「平均値からの各データの差の2乗」の平均値
今度は、それぞれのデータと平均値の差を「2乗」したものの平均を考えます。2乗しているので、この値も必ず0以上となります。この値は「分散(Variance)」と呼ばれ、![]() で表すこともできます。
で表すこともできます。
n個のデータを![]() 、その平均値を
、その平均値を![]() (エックスバー)とすると、分散
(エックスバー)とすると、分散![]() は下の式から求められます。
は下の式から求められます。
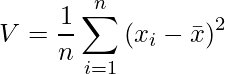
次の順番に従ってデータAとデータBの分散を求めてみます。
- 各データの平均値からの差を求める
- (1)で算出した値をそれぞれ全て2乗する
- (2)で算出した値を全て足す
- (3)で算出した値をデータ数で割る(=分散)
- データAの分散:
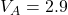
- データBの分散:
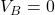
| データA | (1)平均値からの差 | (2)(平均値からの差)2 |
|---|---|---|
| 1 | 2.5 | 6.25 |
| 2 | 1.5 | 2.25 |
| 3 | 0.5 | 0.25 |
| 4 | -0.5 | 0.25 |
| 5 | -1.5 | 2.25 |
| 6 | -2.5 | 6.25 |
| 合計=21 | 合計=0 | (3)合計=17.5 |
| 平均=3.5 | - | (4)分散=17.5/6≒2.9 |
| データB | (1)平均値からの差 | (2)(平均値からの差)2 |
|---|---|---|
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 合計=21 | 合計=0 | (3)合計=0 |
| 平均=3.5 | - | (4)分散=0/6≒0 |
この結果から、データAとデータBの分散は次のようになります。
分散はデータがどの程度平均の周りにばらついているかを表します。分散が小さいほどデータの値は平均値に集まっているということを、逆に大きいほどデータの値が平均値からばらついていることを表します。分散を比較すると、データAのほうがデータBよりもばらついていることが分かります。

【コラム】「偏差」の和はなぜ「0」になるのか?
データの数をn、各データの値を![]() とすると、平均値
とすると、平均値![]() は次の式から算出できます。
は次の式から算出できます。

この式は、下のように変形することができます。

つまり、データの総和は平均値をデータの数だけ足したものと等しくなります。これを用いると、偏差の和は次のように変形できます。

ここで「![]() (各データ)」に①の式を使うと、
(各データ)」に①の式を使うと、
![]()
となり、偏差の和は常に「0」となることが分かります。
6. 分散と標準偏差
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
記述統計量







