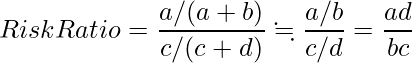- Step2. 中級編
- 1. 2×2のクロス集計表と様々な比率
1-4. オッズ比2
■オッズ比の信頼区間
ある標本調査によって得た次のような2×2分割表を考えます。
| 事象の発生あり | 事象の発生なし | 合計 | |
|---|---|---|---|
| 暴露あり | a | b | a+b |
| 暴露なし | c | d | c+d |
| 合計 | a+c | b+d | a+b+c+d |
このとき、「標本データから算出した暴露なし群における事象の起こりやすさに対する暴露あり群における事象の起こりやすさの値」である標本オッズ比を ![]() とおきます。
とおきます。![]() は次の式から計算できます。
は次の式から計算できます。
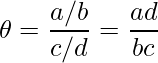
また、母集団のオッズ比(母オッズ比)を ![]() とします。対数オッズ比
とします。対数オッズ比 ![]() の期待値は母対数オッズ比
の期待値は母対数オッズ比 ![]() に等しくなります。
に等しくなります。
母対数オッズ比が平均 ![]() 、分散
、分散 ![]() の正規分布で近似できることを利用すると、母対数オッズ比の95%信頼区間は次の式から求めることができます。
の正規分布で近似できることを利用すると、母対数オッズ比の95%信頼区間は次の式から求めることができます。
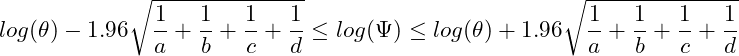
したがって、母オッズ比の95%信頼区間は次の式から求めることができます。
![Rendered by QuickLaTeX.com \displaystyle \theta \times exp \left[-1.96\sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}} \right] \leq \Psi \leq \theta \times exp \left[1.96\sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}} \right]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-ce5191faf828f9d3a2d869243de02e66_l3.png)
- 信頼区間の下限値が1より大きい場合:ある群における事象の起こりやすさが対照群よりも有意に大きい
- 信頼区間の上限値が1より小さい場合:ある群における事象の起こりやすさが対照群よりも有意に小さい
- 信頼区間に1を含む(信頼区間が1をまたぐ)場合:ある群における事象の起こりやすさは対照群とは有意差があるとはいえない
このように、オッズ比に意味があるかどうかを判断するためには、オッズ比と信頼区間を合わせて算出する必要があります。また、論文などに記載する場合には 1.2 [1.05-2.10] のようにオッズ比(この場合1.2)とその信頼区間(この場合、下限値=1.05、上限値=2.10)を併記します。
例題:
ある食品Aを習慣的に摂取していたかが高血圧症の原因であるかどうかを検討するために、高血圧の200人と健常な400人に対して食品Aの習慣的な摂取の有無について調査を行いました。次の表はこの調査の結果をまとめたものです。
この結果を使って、食品A摂取による血圧への効果を評価するためのオッズ比およびオッズ比の信頼区間を計算し、結論を導き出してください。
| 高血圧 | 健常 | 合計 | |
|---|---|---|---|
| 食品Aの習慣的な摂取あり | 80 | 100 | 180 |
| 食品Aの習慣的な摂取なし | 120 | 300 | 420 |
| 合計 | 200 | 400 | 600 |
まずは、標本オッズ比を求めます。
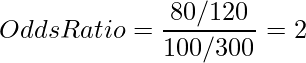
次に、母オッズ比 ![]() の信頼区間を求めます。
の信頼区間を求めます。
![Rendered by QuickLaTeX.com \displaystyle 2 \times exp \left[-1.96\sqrt{\frac{1}{80}+\frac{1}{120}+\frac{1}{100}+\frac{1}{300}} \right] \leq \Psi \leq 2 \times exp \left[1.96\sqrt{\frac{1}{80}+\frac{1}{120}+\frac{1}{100}+\frac{1}{300}} \right]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-be15a5a5f39833be2cca82fd38bf51b3_l3.png)
この結果から、信頼区間の下限値が1より大きい(信頼区間が1をまたがない)ことが分かります。すなわち、食品Aを習慣的に摂取していた群における高血圧症の発症しやすさは、食品Aを習慣的に摂取していない群よりも有意に大きいと結論付けられます。
■オッズ比の性質
- 事象の発生頻度が非常に小さい場合、オッズ比はリスク比の近似値となる
次のような2×2分割表から「暴露なし群に対する暴露あり群の事象発生率の比リスク比」を計算すると、
| 事象の発生あり | 事象の発生なし | 合計 | |
|---|---|---|---|
| 暴露あり | a | b | a+b |
| 暴露なし | c | d | c+d |
| 合計 | a+c | b+d | a+b+c+d |
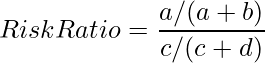
となります。事象の発生頻度が非常に小さい場合、![]() 、
、![]() となるため、オッズ比はリスク比の近似値となります。
となるため、オッズ比はリスク比の近似値となります。