- Step2. 中級編
- 2. 確率分布
2-3. チェビシェフの不等式
■チェビシェフの不等式とは?
チェビシェフの不等式とは確率変数![]() が、平均
が、平均![]() 、分散
、分散![]() の確率分布に従うとき、次の式で与えられる不等式のことです。
の確率分布に従うとき、次の式で与えられる不等式のことです。
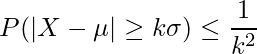
ただし、![]() は任意の値を表します。また、チェビシェフの不等式はどのような確率分布の確率変数
は任意の値を表します。また、チェビシェフの不等式はどのような確率分布の確率変数![]() においても成り立ちます。
においても成り立ちます。
■チェビシェフの不等式の使い方1
![]() 、
、![]() である確率分布について考えます。この確率分布において
である確率分布について考えます。この確率分布において![]() もしくは
もしくは ![]() となる確率を、チェビシェフの不等式を使って求めてみます。
となる確率を、チェビシェフの不等式を使って求めてみます。
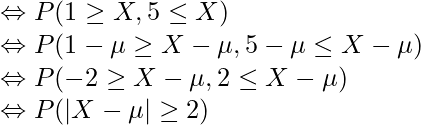
となる確率を求めればよいことが分かります。ここで、チェビシェフの不等式を用います。
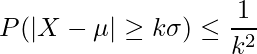
![]() 、
、![]() であることから
であることから
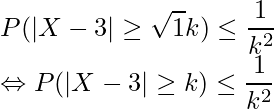
が成り立ちます。これらの式から![]() であることが分かるので、
であることが分かるので、
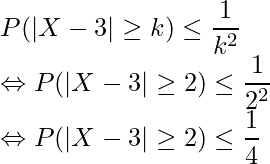
となります。すなわち、![]() もしくは
もしくは ![]() となる確率は
となる確率は ![]() 以下であると考えられます。
以下であると考えられます。
■チェビシェフの不等式の使い方2
![]() 、
、![]() である確率分布について考えます。この確率分布において
である確率分布について考えます。この確率分布において![]() となる確率を、チェビシェフの不等式を使って求めてみます。
となる確率を、チェビシェフの不等式を使って求めてみます。
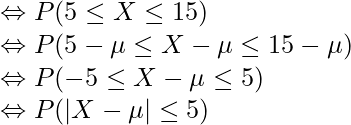
となる確率を求めればよいことが分かります。ここで、チェビシェフの不等式を用います。不等号の向きに注意して、
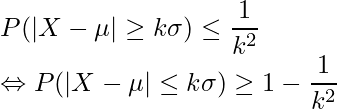
の式を使います。![]() 、
、![]() であることから
であることから
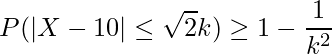
が成り立ちます。これらの式から![]() を用いて
を用いて
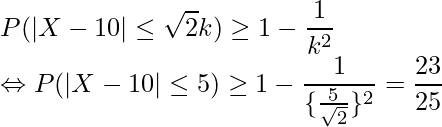
となります。すなわち、![]() となる確率は
となる確率は ![]() 以上であると考えられます。
以上であると考えられます。
■チェビシェフの不等式の証明(離散型確率変数の場合)
離散型確率変数の分散は次の式で計算できます。
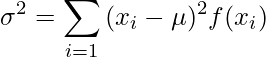
この式を次のように展開します。
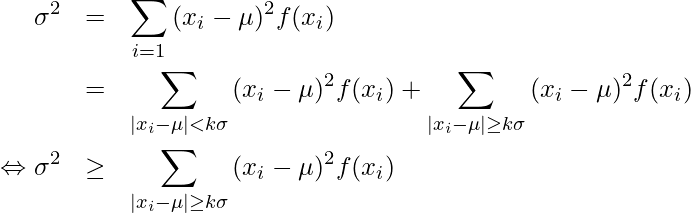
ここで、![]() より
より![]() であることから
であることから
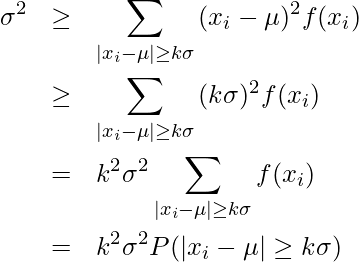
となります。両辺を![]() で割ると、
で割ると、
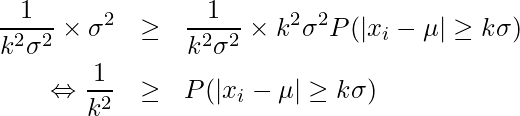
となります。
■チェビシェフの不等式の証明(連続型確率変数の場合)
連続型確率変数の分散は次の式で計算できます。
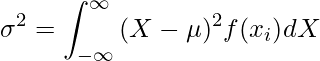
この式を次のように展開します。
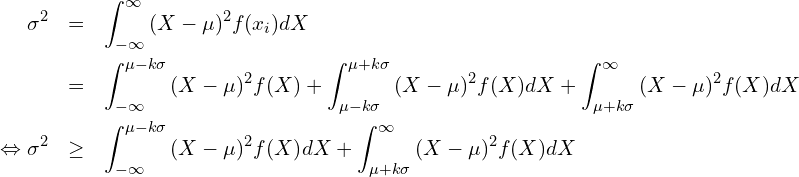
ここで、![]() より
より![]() であることから
であることから
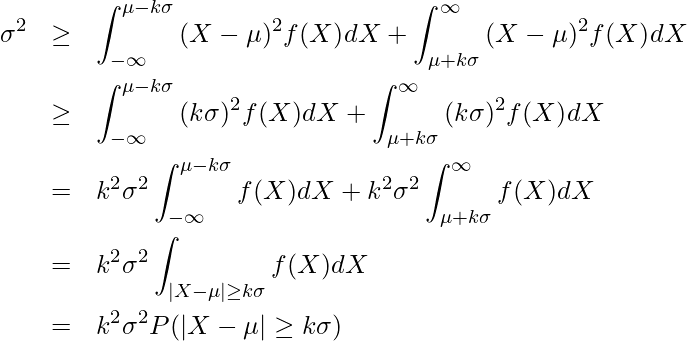
となります。離散型確率変数のときと同様に両辺を![]() で割ると、
で割ると、
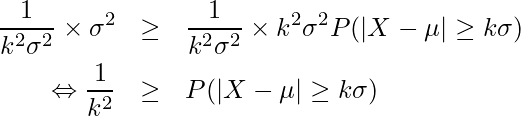
となります。






