- Step2. 中級編
- 7. 重回帰分析
7-1. 重回帰分析1
複数の説明変数を含むデータがある場合、これらを同時に扱う方法として重回帰モデルを考えます。重回帰モデルでは、目的変数 ![]() が複数(ここでは
が複数(ここでは ![]() 個)の説明変数
個)の説明変数 ![]() の線形結合によって表されると仮定します。
の線形結合によって表されると仮定します。
まず、モデル全体を次のように表します。
ここで、![]() は重回帰モデルにおける回帰係数(偏回帰係数)を表します。他の説明変数を一定に保ったときに、説明変数
は重回帰モデルにおける回帰係数(偏回帰係数)を表します。他の説明変数を一定に保ったときに、説明変数 ![]() が1単位変化した時の目的変数
が1単位変化した時の目的変数 ![]() の平均的な変化量を表します。
の平均的な変化量を表します。![]() は誤差項であり、説明変数では説明しきれないばらつきを表します。誤差項は平均0、分散
は誤差項であり、説明変数では説明しきれないばらつきを表します。誤差項は平均0、分散 ![]() の正規分布に従うと仮定します。
の正規分布に従うと仮定します。
■重回帰モデル
![]() 個の説明変数からなる
個の説明変数からなる ![]() 個の観測値がある場合、重回帰モデルは各観測値ごとに次のように表すことができます。
個の観測値がある場合、重回帰モデルは各観測値ごとに次のように表すことができます。
ここで、
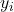 は
は 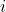 番目の観測値における目的変数
番目の観測値における目的変数 は
は 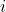 番目の観測値における
番目の観測値における 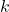 番目の説明変数
番目の説明変数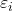 は
は 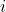 番目の観測値における誤差項
番目の観測値における誤差項
を表します。誤差項 ![]() は互いに独立で、正規分布
は互いに独立で、正規分布 ![]() に従うものとします。
に従うものとします。
この重回帰モデルにおける回帰係数 ![]() を求めるための方法の1つが最小二乗法です。
を求めるための方法の1つが最小二乗法です。
■最小二乗法
最小二乗法とは観測値と予測値の誤差の二乗和が最小になるように、予測値の未知のパラメーターを求める方法のことです。すなわち、重回帰モデルの回帰係数 ![]() は直接観測することができないため、観測値にできるだけ近い予測値を与えるように回帰係数を推定する必要があります。回帰係数の推定値は一般に
は直接観測することができないため、観測値にできるだけ近い予測値を与えるように回帰係数を推定する必要があります。回帰係数の推定値は一般に ![]() と表します。
と表します。
最小二乗法では、![]() 番目の観測値
番目の観測値 ![]() に対する予測値
に対する予測値 ![]() を次のように表すことができます。
を次のように表すことができます。
このとき、実際の観測値 ![]() と予測値
と予測値 ![]() との差を残差と呼び、次のように定義します。
との差を残差と呼び、次のように定義します。
最小二乗法を用いて、残差の平方和(残差平方和) ![]() を最小にする
を最小にする ![]() を計算します。
を計算します。

具体的には ![]() を
を ![]() のそれぞれで偏微分して0とおいた式を使います。
のそれぞれで偏微分して0とおいた式を使います。
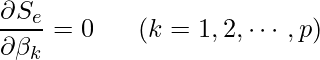
実際に計算すると、次のような連立方程式が得られます。この連立方程式を正規方程式と呼びます。この正規方程式を解くと、各回帰係数の推定値 ![]() が算出できます。このとき得られる回帰係数の推定値
が算出できます。このとき得られる回帰係数の推定値 ![]() を最小二乗推定量(least squares estimator)と呼びます。
を最小二乗推定量(least squares estimator)と呼びます。
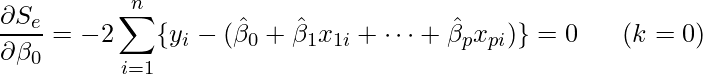
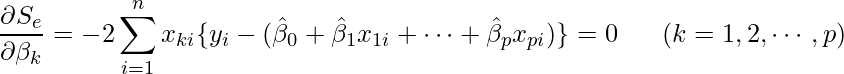
■行列表現による重回帰モデル
説明変数が複数ある場合、行列を使うと式が見やすくなります。まず各記号を次のように定義します。
- 目的変数
- 回帰係数
- デザイン行列
- 誤差項
![Rendered by QuickLaTeX.com \[\mathbf{y}= \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix}\]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-d060dda2abaa1c9dd0d513463c090330_l3.png)
![Rendered by QuickLaTeX.com \[\boldsymbol{\beta}= \begin{pmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{pmatrix}\]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-3f6223e4d84e5babd5938da5bb986132_l3.png)
![Rendered by QuickLaTeX.com \[\mathbf{X}= \begin{pmatrix} 1 & x_{11} & x_{21} & \cdots & x_{p1} \\ 1 & x_{12} & x_{22} & \cdots & x_{p2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{1n} & x_{2n} & \cdots & x_{pn} \end{pmatrix}\]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-8b7a28b08923e145402a2c80f4753116_l3.png)
![Rendered by QuickLaTeX.com \[\boldsymbol{\varepsilon}= \begin{pmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \end{pmatrix}\]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-dd1a5a6d8e3ef74f81aefd94669dc840_l3.png)
これらを用いると、
- 重回帰モデル
- 予測値ベクトル(ただし回帰係数の推定値を
 とします)
とします) - 残差ベクトル
![]()
![]()
![]()
と表すことができます。残差平方和は次のようになります。
![Rendered by QuickLaTeX.com \[S_e = \sum_{i=1}^{n} e_i^2 = \mathbf{e}^\mathsf{T}\mathbf{e} = (\mathbf{y}-\mathbf{X}\boldsymbol{\beta})^\mathsf{T} (\mathbf{y}-\mathbf{X}\boldsymbol{\beta})\]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-3590220acb0387d1f47c5eac973b886e_l3.png)
ここで ![]() を
を ![]() で微分して0とおくと、正規方程式が得られます。
で微分して0とおくと、正規方程式が得られます。
![]()
さらに、![]() が逆行列をもつとき,正規方程式を解くことで、重回帰モデルにおける回帰係数の最小二乗推定量である
が逆行列をもつとき,正規方程式を解くことで、重回帰モデルにおける回帰係数の最小二乗推定量である ![]() が算出できます。
が算出できます。
![]()
正規方程式 ![]() は、残差ベクトル
は、残差ベクトル ![]() が
が ![]() の各列(切片列を含む)と直交することを意味します。
の各列(切片列を含む)と直交することを意味します。
■重回帰モデルにおける仮定
これまでに示した最小二乗解が統計的に意味をもつためには、重回帰モデルに対していくつかの仮定を置く必要があります。以下に基本的な仮定をまとめます。
- 誤差項
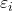 の期待値は
の期待値は 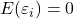
- 誤差項の分散は一定である(等分散性)
- 誤差項は互いに独立である
- 誤差項は正規分布
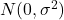 に従う
に従う - 説明変数間に完全な線形従属が存在しない(
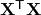 が逆行列をもつ)
が逆行列をもつ)
上記の仮定のもとで,最小二乗推定量 ![]() は不偏であり,分散が最小となります(Gauss–Markov 定理)。
は不偏であり,分散が最小となります(Gauss–Markov 定理)。
■決定係数
目的変数 ![]() の変動である全変動の平方和
の変動である全変動の平方和 ![]() は次のように計算できます。
は次のように計算できます。![]() は
は ![]() 全体の平均です。
全体の平均です。
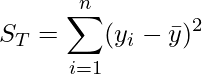
また、残差平方和 ![]() は次のように計算できます。
は次のように計算できます。
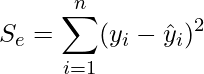
これらを用いると、決定係数 ![]() は次の式で定義されます。
は次の式で定義されます。
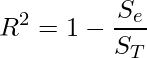
![]() は目的変数の変動のうち,回帰モデルによって説明される割合を表します。説明変数の個数が増えると
は目的変数の変動のうち,回帰モデルによって説明される割合を表します。説明変数の個数が増えると ![]() は必ず増加するため,モデルの複雑さを考慮した指標として自由度調整済み決定係数
は必ず増加するため,モデルの複雑さを考慮した指標として自由度調整済み決定係数 ![]() を用います。
を用います。
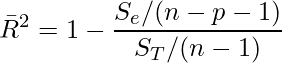
ここまでの説明を行列で表してみます。行列で扱うために、平均からの偏差ベクトルを定義します。目的変数ベクトルを平均で中心化したものを
![]()
とします。ここで ![]() はすべての要素が1の
はすべての要素が1の ![]() 次元ベクトルです。すると、全変動の平方和は次のように計算できます。
次元ベクトルです。すると、全変動の平方和は次のように計算できます。
最小二乗解による予測値 ![]() を射影行列で書くと
を射影行列で書くと
![]()
ここで ![]() は
は ![]() の列空間への直交射影行列です。残差ベクトルは
の列空間への直交射影行列です。残差ベクトルは ![]() であることから、残差の平方和は次のように計算できます。
であることから、残差の平方和は次のように計算できます。
![]()
以上を用いると,決定係数 ![]() は次のように書けます。
は次のように書けます。
![Rendered by QuickLaTeX.com \[R^2 = 1 - \frac{\mathbf{y}^\mathsf{T}(\mathbf{I}-\mathbf{P})\mathbf{y}} {\tilde{\mathbf{y}}^\mathsf{T}\tilde{\mathbf{y}}}\]](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-113c5e6c4476c0bdc1bbf2263589e001_l3.png)
決定係数 ![]() は、目的変数ベクトル
は、目的変数ベクトル ![]() の全変動のうち、デザイン行列
の全変動のうち、デザイン行列 ![]() の張る部分空間への直交射影によって説明される割合を表していると解釈できます。
の張る部分空間への直交射影によって説明される割合を表していると解釈できます。







