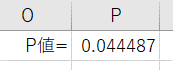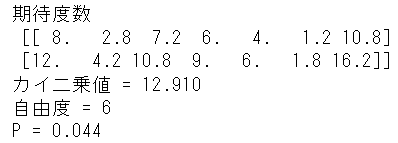- Step3. 実践編
- 2. 推定と検定
2-2. 独立性の検定
次のデータは、「Step0. 初級編 1-1. データをとってみよう」で用いたデータです。このデータを使って、性別間での毛色のちがいについて独立性の検定を行ってみましょう。
ファイルのダウンロードはこちらから
- (日本語)neko_1nensei.csv
- (英語)neko_1nensei_eng.csv
■Excelによる解析例
- 性別と毛色の集計表を作るための枠組みを作成
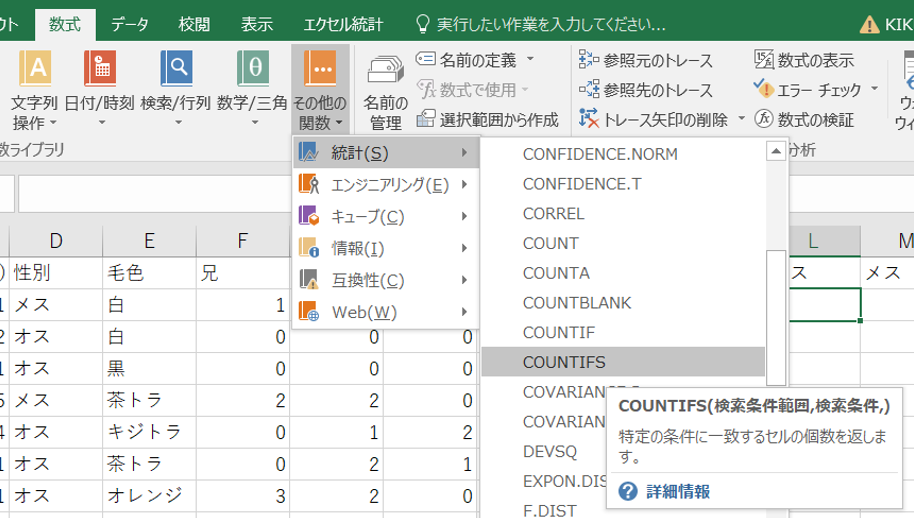
- 「白・オス」のセルを選択し、数式 > 関数ライブラリの「その他の関数」 > 統計 > COUNTIFSを選択
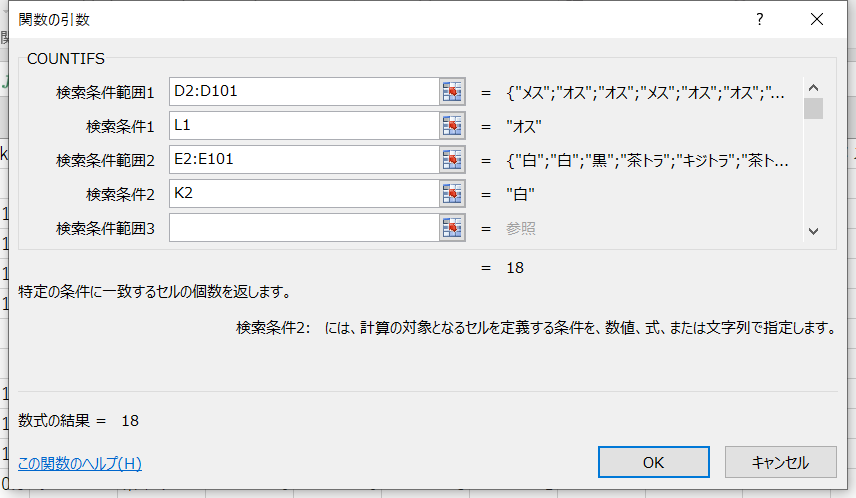
- 「関数の引数」を図のように設定 > [OK]をクリック
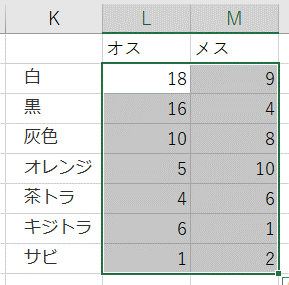
- 値が入力されたのを確認し(「白・オス=18」)、Excel関数を次のように加工
- オートフィルで他のセルの値を自動入力
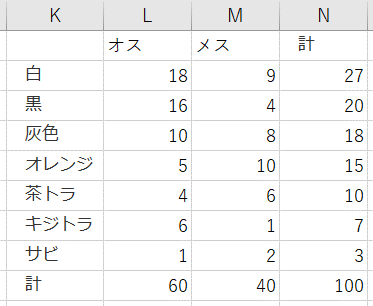
- 行と列の合計値を算出
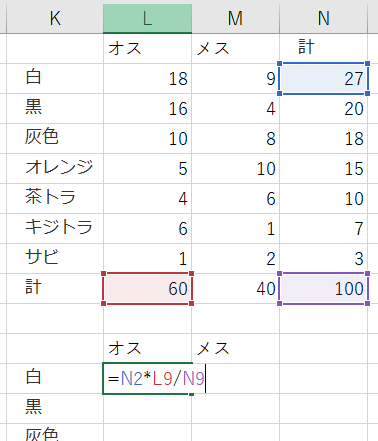
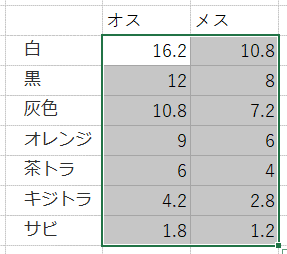
- 期待度数を求める
- 値が入力されたのを確認し(「白・オスの期待度数=16.2」)、Excel関数を次のように加工
- オートフィルで他のセルの値を自動入力
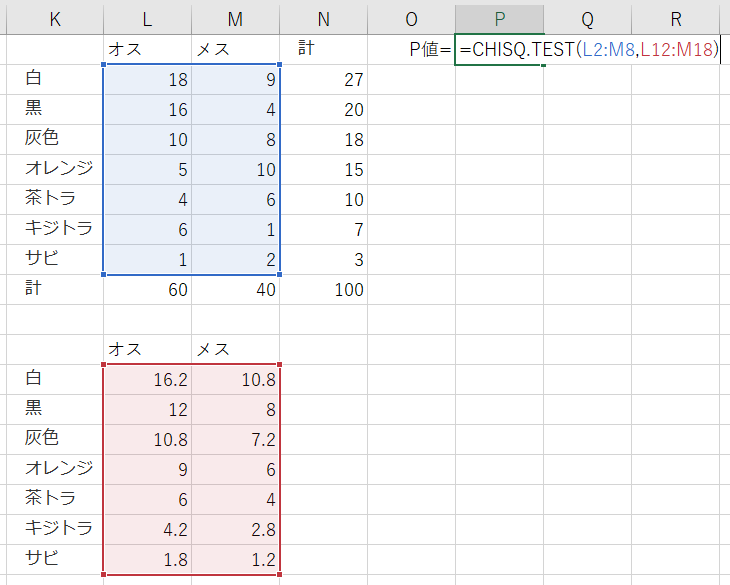
- 観測度数(L2セルからM8セル)と期待度数(L12セルからM18セル)を選択し、「CHISQ.TEST」関数を用いて独立性の検定を行う
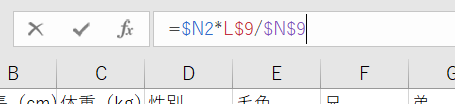
※オートフィルで値が自動入力されるように、セルの参照位置を「$」で調整します。
※各セルの期待度数は行の和と列の和の積をすべての度数の和で割ったものになります。例えば「白・オス」の期待度数はで求められます。
※オートフィルで値が自動入力されるように、セルの参照位置を「$」で調整します。
※独立性の検定の結果P=0.044となり、有意水準5%の片側検定において「性別と毛色は独立ではない(関連がある)」と結論付けられます。
■Rによる解析例
この検定では、2標本の等分散を仮定しないWelchのt検定(両側検定)を行います。
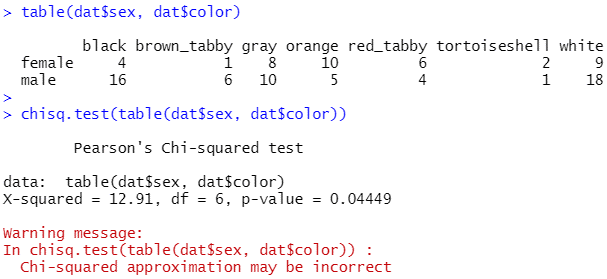
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | dat <- read.csv("neko_1nensei_eng.csv", header=T)head(dat) #データの確認(データの先頭6行を表示)table(dat$sex, dat$color) #sexとcolorの集計表を作成 #カイ二乗検定においてイェーツの補正を行う場合chisq.test(table(dat$sex, dat$color)) #作成した集計表をを使ってカイ二乗検定res <- chisq.test(table(dat$sex, dat$color))res$expected #カイ二乗検定の結果から期待度数を算出#カイ二乗検定においてイェーツの補正を行わない場合chisq.test(table(dat$sex, dat$color), correct=T)#フィッシャーの正確確率検定を行う場合fisher.test(table(dat$sex, dat$color)) |
Rでカイ二乗検定を行うと、以下のような警告が出る場合があります。これは「期待度数が5未満のセル」がある場合に、カイ二乗検定の結果が正確ではない可能性があるということを知らせるための警告です。このような場合にはfisher.testを使ってフィッシャーの正確検定を行います。
■Pythonによる解析例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | import pandas as pdimport scipy as spfrom scipy import statsdat = pd.read_csv("neko_1nensei_eng.csv")crossed = pd.crosstab(dat["sex"], dat["color"]) #sexとcolorの集計表を作成 #カイ二乗検定においてイェーツの補正を行う場合chi2, p, dof, exp = stats.chi2_contingency(crossed)print("期待度数", "\n", exp)print(f'カイ二乗値 = {chi2:.3f}')print(f'自由度 = {dof:d}')print(f'P = {p:.3f}')#カイ二乗検定においてイェーツの補正を行わない場合chi2, p, dof, exp = stats.chi2_contingency(crossed, correction=False) |
pythonでフィッシャーの正確確率検定を行う場合には「p = stats.fisher_exact(crossed)」とします。ただし、集計表が2×2である場合のみ使うことができます。