8-3. 条件付き確率を求めてみよう

学習発表会は猛練習のおかげで大成功だったようです。本番直前は緊張のあまりぶるぶると震えている猫たちがたくさんいましたが、観客から割れんばかりの拍手をもらうと皆満面の笑顔を浮かべてステージを後にしたのでした。

1年生は他の学年の発表も食い入るように見つめ、大いに興味を持ったようです。次の表は1年生100匹が来年の学習発表会でやってみたいと思ったことを集計したものです。

この結果を元に、100匹の中からランダムに選ばれた1匹が「劇をやってみたい」と答える確率は次のように計算できます。

$\displaystyle \frac{10+10}{100} = \frac{20}{100} = \frac{1}{5}$

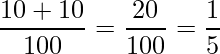
もし、100匹の中からランダムに選ばれた1匹がオスであったときに、その1匹が「劇をやってみたい」と答える確率は次のように計算できます。

$\displaystyle \frac{10}{60} = \frac{1}{6}$

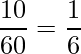
このように、何か条件がある場合の確率のことを「条件付き確率」といいます。条件付き確率は次の式から求められます。

$\displaystyle P(B|A) = \frac{P(A \cap B)}{P(A)}$

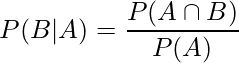
このとき、P(B|A)は「Aという条件のもとでBが起こる確率」を、P(A∩B)は「AかつBが起こる確率」を、P(A)は「Aが起こる確率」を表します。

上に挙げた結果を使って実際に計算してみます。100匹の中からランダムに選ばれた1匹がオスであったとき（Aという事象とします）に、選ばれた1匹が「劇をやってみたい」と答える（Bという事象とします）確率をP(B|A)とします。ランダムに選ばれた1匹がオスである確率P(A)は

$\displaystyle P(A)= \frac{60}{100} = \frac{3}{5}$

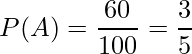
であり、ランダムに選ばれた1匹が「オス」かつ「劇をやってみたい」と答える確率P(A∩B)は、

$\displaystyle P(A \cap B)= \frac{10}{100} = \frac{1}{10}$

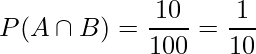
であることから、求める確率P(B|A)は次のように計算できます。

$\displaystyle P(B|A)= \frac{\frac{1}{10}}{\frac{3}{5}} = \frac{1}{6}$

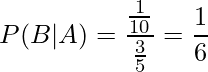
同様にして、100匹の中からランダムに選ばれた1匹が「ダンスをやってみたい」と答えるとき（Aという事象とします）、選ばれた1匹がメスである（Bという事象とします）確率P(B|A)を求めると、

$\displaystyle P(B|A) = \frac{\frac{15}{100}}{\frac{15+15}{100}} = \frac{\frac{15}{100}}{\frac{30}{100}} = \frac{1}{2}$

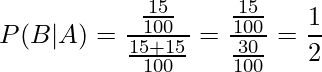
となります。