- Step0. 初級編
- 8. 確率の計算
8-2. いろいろな確率を求めよう
合唱の練習と並行して、合奏の練習も行わなくてはなりません。そこで1年生100匹が音楽室に集まり、どの楽器を担当するかを決めることになりました。
次の表は、1年生100匹の楽器の割り当てをまとめたものです。
| 楽器 | 割り当て匹数 |
|---|---|
| ピアニカ | 53 |
| タンバリン | 12 |
| すず | 10 |
| カスタネット | 15 |
| 木琴 | 7 |
| 小太鼓 | 2 |
| 大太鼓 | 1 |
上に挙げた7種類の楽器の中から担当する楽器がランダムに選ばれる場合、ある猫が担当する楽器がタンバリンである確率P(A)は次のように計算できます。
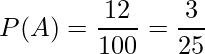
また、ある猫が担当する楽器がタンバリン以外である確率は次のようになります。
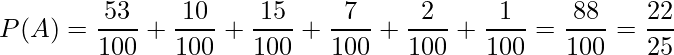
ただし、「事象Aが起こる確率」は「1-事象Aが起こらない確率」として計算することができます。つまり、「ある猫が担当する楽器がタンバリン以外である確率」=「1-『ある猫が担当する楽器がタンバリンである確率』」となるので、
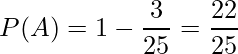
と計算することもできます。
音楽室の隅に、小太鼓と大太鼓を希望する猫たちが集まってきました。小太鼓は2匹、大太鼓は1匹が担当できます。小太鼓を希望する猫は4匹(もち、ふく、あずき、しま)、大太鼓を希望する猫も4匹(のっぽ、ぶち、だいず、たま)のようです。実は「あずき」と「だいず」は双子の猫です。この2匹がそれぞれ小太鼓と大太鼓を担当する確率を求めてみます。
「もち、ふく、あずき、しま」の中から、2匹が選ばれるすべての組み合わせは「もち-ふく」「もち-あずき」「もち-しま」「ふく-あずき」「ふく-しま」「あずき-しま」の6通りです。このうち「あずき」が含まれるのは3通りなので、小太鼓希望の「あずき」が小太鼓担当となる確率P(A)は、次のようになります。
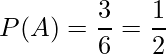
また、大太鼓希望の「だいず」が大太鼓担当となる確率P(A)は、次のようになります。
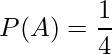
小太鼓担当は小太鼓希望の4匹の猫だけで、大太鼓担当は大太鼓希望の4匹の猫だけで決めるので、小太鼓の担当猫決めの結果が大太鼓の担当猫決めの結果に影響を与えることはありません。同様に、大太鼓の担当猫決めの結果が小太鼓の担当猫決めの結果に影響を与えることはありません。このように、お互いの結果が影響しあうことがないとき、2つの事象は「独立である」と言います。
2つの事象が独立である場合、2つの事象が同時に起こる確率はそれぞれの事象の確率の積で計算することができます。したがって、「あずき」と「だいず」がそれぞれ小太鼓と大太鼓を担当する確率は次のようになります。
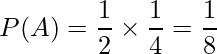
一方、木琴を希望する猫たちは全部で8匹いるようです。公平にじゃんけんをしてみた結果、6匹が勝ち、2匹(とら、ちゃちゃ)が負けてしまいました。残り1匹の木琴担当をかけて、2匹でじゃんけんを続けることになりました。
ただし、2匹の間で「じゃんけんで先に2回勝った方を勝ちとする。じゃんけんは勝負がつくまで行う(あいこは無し)。」という取り決めが交わされました。じゃんけん1回ごとの結果はそれぞれ「独立」なので、じゃんけんを繰り返し行った結果の確率は、1回ごとの結果の確率の積で求めることができます。じゃんけんを1回行うとき、「とらが勝つ確率」=「ちゃちゃが勝つ確率」=![]() です。
です。
ここではとらが勝つ確率について求めてみます。この場合、①とらが2連勝する、もしくは、②とらが2勝1敗する、のどちらかになります。
- ①とらが2連勝する場合
- ②とらが2勝1敗する場合
- 勝ち-負け-勝ち
- 負け-勝ち-勝ち
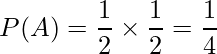
とらが2勝1敗する場合というのは、3回目のじゃんけんでとらの勝ちが決まる場合です。この場合、次の2パターンが考えられます。
それぞれのパターンの確率は、次のように計算できます。
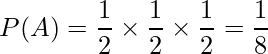
したがって、とらが勝つ確率は、①と②の確率をすべて足して
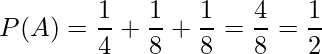
となります。






