- Step0. 初級編
- 5. データのばらつき
5-1. データのばらつきを計算してみよう
真っ青な空に真っ白な入道雲が浮かぶ8月―――一年で一番の大イベント、夏休みが始まりました。どっさりと机に積まれた宿題なんて何のその。皆朝早くから夜遅くまで気ままに活動しているようです。今日はそんな猫たちの一日を少しだけ覗いてみます。
【朝はラジオ体操】朝6時半から始まるラジオ体操は、校区内の様々な場所で行われています。次の表は山のふもと町内の2つの公園で行われているラジオ体操の参加数をまとめたものです。
| 日付 | ねこじゃらし公園 | またたび公園 |
|---|---|---|
| 8月1日 | 40 | 50 |
| 8月2日 | 35 | 30 |
| 8月3日 | 30 | 60 |
| 8月4日 | 25 | 25 |
| 8月5日 | 30 | 65 |
比較のため、2つの公園における1日当たりの参加数の平均値を求めてみます。
| ねこじゃらし公園 | またたび公園 | |
|---|---|---|
| 平均 | 32 | 46 |
この結果より、またたび公園のほうが平均参加数が多いことが確認できます。次に、このデータからグラフを作ってみます。時系列のデータなので、3-2章で学んだ折れ線グラフを使います。
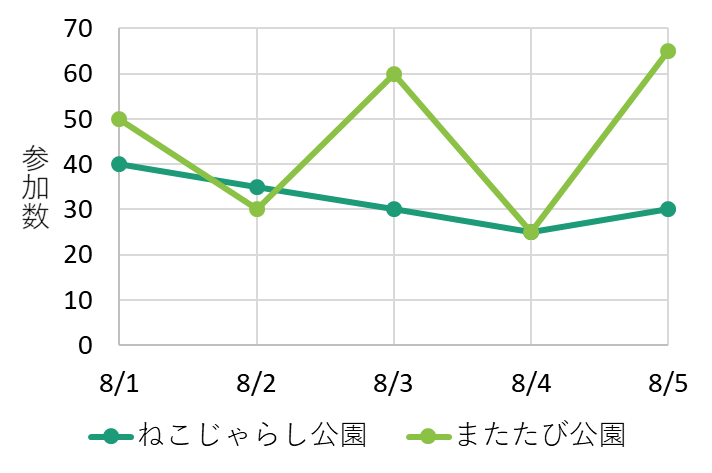
この図を見ると、ねこじゃらし公園に比べてまたたび公園の参加数は日によってかなりばらつきがあることが分かります。このばらつきを表すための値が「分散」と「標準偏差」です。ばらつきが大きいほど、「分散」も「標準偏差」も大きな値をとります。
■分散の求め方
分散は次の手順に従って求めます。
- 各データと平均値の差を求める
- 1で求めた値を2乗する
- 2で求めた値をすべて足す
- 3で求めた値をサンプルの数で割る
まず、ねこじゃらし公園の参加数の分散を求めてみます。
| 日付 | ねこじゃらし公園 | 1. 各データと平均値の差 | 2. (各データと平均値の差)の2乗 |
|---|---|---|---|
| 8月1日 | 40 | 40-32=8 | 82=64 |
| 8月2日 | 35 | 35-32=3 | 32=9 |
| 8月3日 | 30 | 30-32=-2 | (-2)2=4 |
| 8月4日 | 25 | 25-32=-7 | (-7)2=49 |
| 8月5日 | 30 | 30-32=-2 | (-2)2=4 |
3. (各データと平均値の差)の2乗の和=64+9+4+49+4=130
4. ねこじゃらし公園の参加数の分散=130÷5=26 となります。
次に、またたび公園の参加数の分散を求めてみます。今度は式を使って計算してみます。
またたび公園の参加数の分散={(50-46)2+(30-46)2+(60-46)2+(25-46)2+(65-46)2}÷5
={42+(-16)2+142+(-21)2+(19)2}÷5
={16+256+196+441+361}÷5
=1270÷5=254 となります。
■標準偏差の求め方
標準偏差は次の手順に従って求めます。
- 分散を求める
- 1で求めた値のルート(正の平方根)をとる
ねこじゃらし公園の参加数の標準偏差=√26=5.1
またたび公園の参加数の標準偏差=√254=15.9
ここまでの結果をまとめると次のようになります。この結果を見ても、またたび公園の参加数のほうがばらつきが大きいことが分かります。
| ねこじゃらし公園 | またたび公園 | |
|---|---|---|
| 分散 | 26 | 254 |
| 標準偏差 | 5.1 | 15.9 |
上に書いた式からも分かるように、分散も標準偏差もどちらも必ず0以上の値をとります。すべてのデータが平均値である場合(すべてのデータが同じである場合)には、分散も標準偏差もどちらも0になります。







