- Step0. 初級編
- 8. 確率の計算
8-1. 確率を求めてみよう
赤い葉や黄色い葉が美しく色づく11月―――学習発表会に向けて、歌や合奏の練習に熱が入ります。ちょうど先週、1年生の合唱曲が「世界中のこねこたちが」に決まったのです。
次の表は、1年生の合唱曲の候補となっていた曲をまとめたものです。
| 候補No. | 曲名 |
|---|---|
| 1 | 気球に乗ってどこへでも |
| 2 | おさんぽ |
| 3 | 世界中のこねこたちが |
| 4 | 肉球を太陽に |
| 5 | 歌えにゃんにゃん |
| 6 | 恐竜のバラード |
これらの候補曲の中から1曲が1年生の合唱曲として選ばれる確率について考えてみます。「確率」とは、物事の「起こりやすさ」を定量的に表す指標のことです。また、この「物事」のことを「事象(じしょう)」といいます。
いくつかの事象の起こりやすさがすべて等しいとき、「同様に確からしい」といいます。このとき、ある事象Aが起こる確率P(A)は次の式から計算できます。
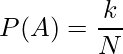
Nは「起こりうるすべての場合の数」を、kは「事象Aが起こる場合の数」を表しています。
合唱曲は、この6曲の中からくじ引きで決めました。したがって、6曲のうちどの曲が選ばれる確率も等しいと考えられます。この6曲の中から「世界中のこねこたちが」が選ばれる(=事象A)という確率(=P(A))は、
- 「起こりうるすべての場合の数」=「候補曲の数」=「6」
- 「事象Aが起こる場合の数」=「『世界中のこねこたちが』が選ばれる場合の数」=「1」
を用いて
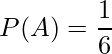
と計算できます。
合唱曲が無事に決まったので、次に指揮者を決めることになりました。指揮者は立候補制で、8匹の猫たちが立候補をしました(くろ、たま、ぶち、モカ、みみ、まる、ぷく、もも)。この中からくじ引きで1匹を選びました。このとき、「ぷく」が選ばれる確率P(A)は
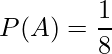
となります。
また、合唱の伴奏者も決めました。立候補した4匹の猫(しろ、みけ、そら、うみ)の中からくじ引きで2匹を選びました。
4匹の中から2匹が選ばれるすべて場合の数は、次の表で示すとおり6です。
| 組み合わせNo. | 伴奏者 |
|---|---|
| 1 | しろ-みけ |
| 2 | しろ-そら |
| 3 | しろ-うみ |
| 4 | みけ-そら |
| 5 | みけ-うみ |
| 6 | そら-うみ |
このとき、「しろ」と「みけ」が選ばれる確率P(A)は
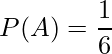
となります。






