- Step0. 初級編
- 6. データの標準化
6-3. 偏差値を求めてみよう
6-2章で算出した標準化したデータをより分かりやすくするために、「偏差値」を計算する場合があります。偏差値は、元のデータを平均が50、標準偏差が10となるように変換した値のことです。具体的には、標準化した値を10倍して50を足すことで求められます。
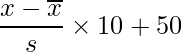
![]() は元のデータを、
は元のデータを、![]() は平均値を、
は平均値を、![]() は標準偏差を表します。例えば、「くろ」の「ボール投げ」のデータから偏差値を計算すると次のようになります。
は標準偏差を表します。例えば、「くろ」の「ボール投げ」のデータから偏差値を計算すると次のようになります。
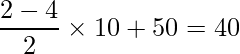
同様にしてすべてのデータから偏差値を求めると次のようになります。
| 競技名 | くろ | しま | みけ |
|---|---|---|---|
| ボール投げ | 40 | 45 | 50 |
| 走り幅跳び | 90 | 40 | 50 |
| 50m走 | 79 | 37 | 46 |
| 高跳び | 50 | 25 | 88 |
| 木登り | 52 | 48 | 68 |
■偏差値の特徴
・偏差値が高いほど成績が良いことを、低いほど成績が悪いことを表します。
・平均点と同じ点数だった場合、偏差値は50になります。これは、平均点と同じ点数の場合には標準化した値が0となるためです。
・異なる科目や競技で同じ点数だった場合でも、偏差値は等しくなるとは限りません。その科目や競技の平均値や標準偏差が異なる場合には、偏差値は異なったものになります。
・偏差値は100以上の値やマイナスの値をとる場合があります。標準偏差が小さく、平均値からかけ離れた点数を取った場合には偏差値は非常に大きな値や小さな値をとります。







