- Step0. 初級編
- 4. 代表値と箱ひげ図
4-1. 平均、中央値、最頻値を求めてみよう
日差しの強い7月―――今日は猫稲荷神社のお祭りです。神社の境内にはたくさんの屋台が並んでいます。町中の猫たちが陽気な祭囃子に誘われて続々と集まってきています。
■平均
どれもこれも魅力的に見えてしまう屋台ですが、子猫たちは自分のお小遣いと相談しながら何を買おうか吟味しているようです。次の表はランダムに選んだ5匹の子猫のお小遣いの金額を集計したものです。
| 名前 | お小遣いの金額(円) |
|---|---|
| ちび | 1000 |
| はな | 500 |
| たま | 700 |
| そら | 1200 |
| くろ | 800 |
「平均」とはすべてのデータを足してデータの数で割ったものです。この表からお小遣いの金額の平均を計算すると次のようになります。
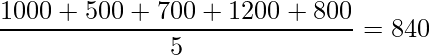
■中央値
屋台の中にはたくさんの猫たちが並んでいる屋台もあれば、そうでない屋台もあります。次の表はランダムに選んだ10軒の屋台に並んでいる猫の数を集計したものです。
| 出店 | 並んでいる猫の数(匹) |
|---|---|
| わたがし | 3 |
| 焼き鳥 | 1 |
| 金魚すくい | 10 |
| たこ焼き | 6 |
| 射的 | 0 |
| リンゴ飴 | 7 |
| 焼きトウモロコシ | 2 |
| かき氷 | 12 |
| 水ヨーヨー | 8 |
| くじ引き | 7 |
このデータから「中央値」を求めてみます。中央値とはデータを小さい順に並べたデータのちょうど中央にあるデータのことです。
まず、上のデータを小さい順に並べ替えてみます。
| 出店 | 並んでいる猫の数(匹) |
|---|---|
| 射的 | 0 |
| 焼き鳥 | 1 |
| 焼きトウモロコシ | 2 |
| わたあめ | 3 |
| たこ焼き | 6 |
| リンゴ飴 | 7 |
| くじ引き | 7 |
| 水ヨーヨー | 8 |
| 金魚すくい | 10 |
| かき氷 | 12 |
データが奇数個(5個、7個など)の場合はちょうど真ん中にくる値が中央値となりますが、上のデータのようにデータが偶数個(4個、6個など)の場合はちょうど真ん中にくる値がありません。そこで偶数個の場合には、中央に最も近い2つの値の平均値を中央値とします。
このデータでは、「たこ焼き:6匹」と「リンゴ飴:7匹」が中央に最も近い2つの値です。したがって中央値は(6+7)÷2=6.5となります。
■最頻値
猫たちにとってやっぱり一番魅力的なのは食べ物の屋台のようです。次の表は13軒の屋台が出している食べ物の値段をまとめたものです。
| 出店 | 値段(円) |
|---|---|
| はし巻き | 300 |
| 焼き鳥 | 100 |
| 焼きトウモロコシ | 200 |
| わたあめ | 100 |
| たこ焼き | 400 |
| りんご飴 | 150 |
| たい焼き | 100 |
| チョコバナナ | 200 |
| わらび餅 | 200 |
| ラムネ | 150 |
| ポップコーン | 200 |
| 水あめ | 50 |
| アユの塩焼き | 300 |
「最頻値」は「モード」ともよばれ、最も頻度が高い値(一番多く出現している値)を指します。上データを値段ごとに集計すると次のようになります。
| 値段(円) | 度数 |
|---|---|
| 50 | 1 |
| 100 | 3 |
| 150 | 2 |
| 200 | 4 |
| 300 | 2 |
| 400 | 1 |
したがって、最頻値は200円になります。







