- Step1. 基礎編
- 32. その他
32-3. 時系列データと移動平均
データの中には株価や気温の変化、朝顔の成長記録など、「時間」と「その時間に記録された値」からなるものがあります。このような時間の経過に従って測定されたデータのことを「時系列データ」といいます。時系列データを使って、時間の経過による値の変化を分析することを「時系列分析」といいます。時系列分析によって何らかの傾向が見られた場合、その傾向から将来の予測を行うことができます。
株価や気温など時間で細かく変化するデータを眺めると、変動が細かすぎて全体の傾向を掴みにくい場合があります。そのようなときには「移動平均」を用いることで、変化をより滑らかにしてデータを俯瞰できます。
次のデータは、2015年8月の新宿御苑における1時間ごとの気温の測定結果です。毎時データなので、日中と夜間の気温変化を読み取ることはできますが、8月全体を通しての変動は簡単には読み取れそうにありません。

このような場合には、移動平均を取るとデータが見やすくなります。次のグラフは区間数24の移動平均を取ったものです。このグラフを見ると、8月上旬は気温が高く、その後9月に近づくにつれて気温が低下しているということが分かります。

■移動平均の求め方
最も簡単な移動平均は、直近データの単純相加平均を計算することによって求められます。具体的には、移動平均を求めたい中心となるデータから前後のいくつかのデータ(項)を足して、平均をとるという方法です。前後いくつ分の項を考慮するかは場合によって異なり、「区間数n」や「n項移動平均」といった記述によりその数を表します。区間数がnのとき、全部でn個分の項の平均を計算します。
例えば、次のように1から10までの連番データがあった場合に、5番目の項の3項移動平均![]() は次のように求められます。
は次のように求められます。

移動平均の計算方法は、移動平均を取る区間が奇数か偶数かによって異なります。5項移動平均は、中心となる項から前後2個ずつの項を足して、5で割ると計算できます。一方で6項移動平均は、中心となる項から前後3個ずつの項を足していますが、一番離れている![]() と
と![]() についてはどちらも0.5倍されています。
についてはどちらも0.5倍されています。
- 5項の移動平均の式
- 6項の移動平均の式
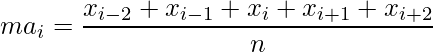
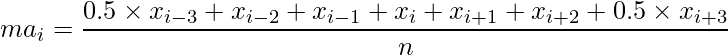
このように偶数の場合は、一番離れている項については0.5倍して計算する必要があります。
■移動平均の計算方法のまとめ(Nが奇数のとき)
![]() となるような
となるような![]() を用いて表すと次のようになります。
を用いて表すと次のようになります。
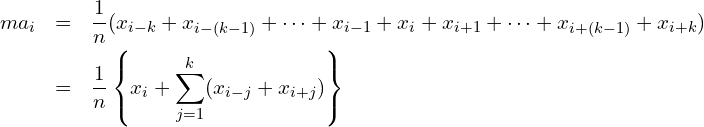
■移動平均の計算方法のまとめ(Nが偶数のとき)
![]() となるような
となるような![]() を用いて表すと次のようになります。
を用いて表すと次のようになります。
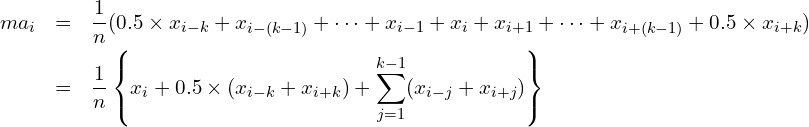
移動平均は前後の項がないと計算することができないので、下表に示すようにデータの始めから![]() 個分と終わり
個分と終わり![]() 個分の移動平均値は存在しません。
個分の移動平均値は存在しません。
| 元データ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 3項移動平均 | - | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | - |
■おすすめ書籍
基礎統計学の本ですが、一般的な基礎統計学の内容(推定、検定、回帰)に加えて時系列分析などについても網羅しています。








