- Step0. 初級編
- 7. データの相関
7-2. データの相関を見てみよう
7-1章で、「参加匹数の多い競技ほど競技時間が長く、また怪我をした猫の数も多い傾向がある」ということが分かりました。具体的にどのくらい強い関係があるのかを見るために、この章では「相関係数」を求めてみます。
相関係数を求めるにあたって、まず2種類のデータのみをグラフに表してみます。データは7-1章に掲載したものを使います。
| 競技 | 参加匹数 | 競技時間(分) | 怪我した猫(匹) |
|---|---|---|---|
| 玉入れ | 100 | 20 | 4 |
| 綱引き | 150 | 30 | 8 |
| リレー | 50 | 15 | 1 |
| 毛糸玉ころがし | 75 | 25 | 5 |
| にぼし食い競走 | 60 | 30 | 5 |
| ムカデ競争 | 125 | 35 | 9 |
| 騎馬戦 | 200 | 40 | 15 |
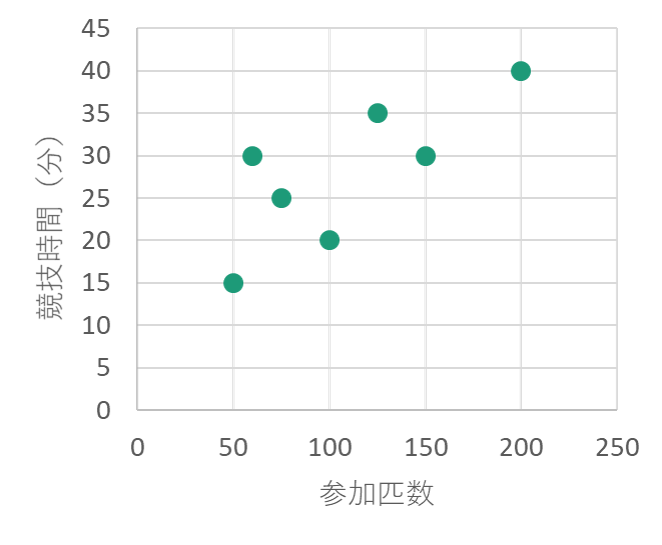
各競技の参加匹数と競技時間をプロットすると次のようになります。
このようなグラフは「散布図」とよばれ、x軸(横軸)で1つ目のデータを、y軸(縦軸)で2つ目のデータを表します。
ここで示したデータのように、横軸の値(参加匹数)が増加すると縦軸の値(競技時間)も増加するという関係がある場合には「正の相関関係がある」といいます。逆に、横軸の値が増加すると縦軸の値は減少するという関係がある場合には「負の相関関係がある」といいます。
では、いよいよ相関係数を求めてみます。2つの要素xとyからなるn個のデータが得られたとき、その相関関係の強弱を表す相関係数![]() は次の式から求められます。
は次の式から求められます。
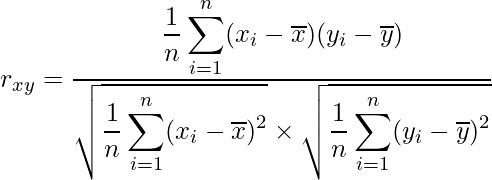
nはサンプルの数を、![]() と
と![]() はi番目のデータの値を、
はi番目のデータの値を、![]() と
と![]() はxとyのデータの平均値を表します。また、
はxとyのデータの平均値を表します。また、![]() はi=1からi=nまでの値をすべて足したものということを意味します。
はi=1からi=nまでの値をすべて足したものということを意味します。
非常に複雑な式なので、実際の値を使って計算してみます。xを参加匹数、yを競技時間とします。それぞれの平均値は![]() =108.6と
=108.6と![]() =27.9です。
=27.9です。
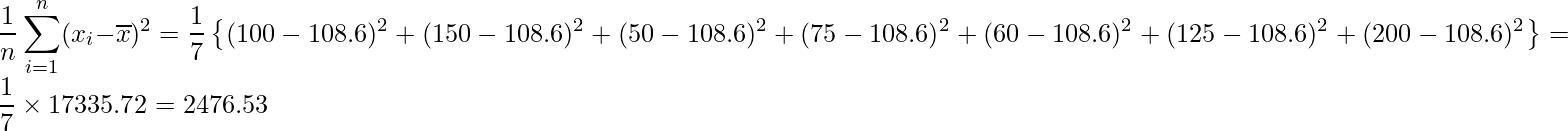
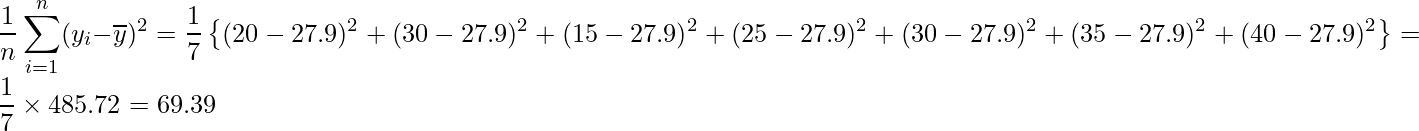
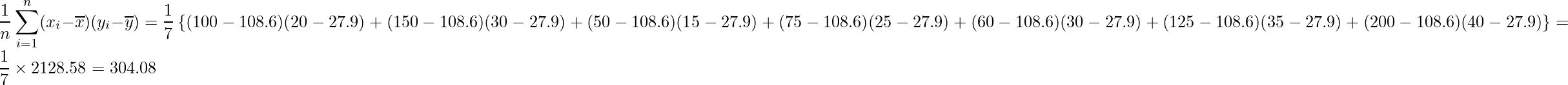
これらの値を使うと、相関係数は
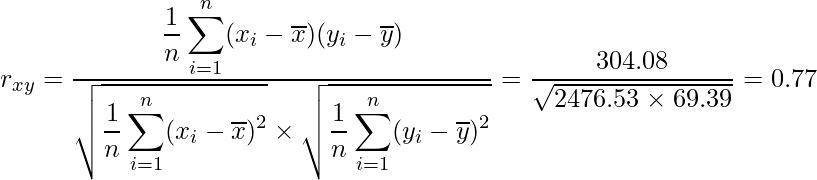
と計算できます。この結果から、参加匹数と競技時間の間には非常に強い相関があることが分かります。
2つのデータの間に強い正の相関があるほど相関係数は1に近づきます。逆に、強い負の相関があるほど相関係数は-1に近づきます。また、相関が弱い場合には相関係数は0に近づきます。